Métodos basados en el conocimiento

Los métodos basados en el conocimiento, tambien denominados heurísticos, determinan la susceptibilidad y/o amenaza directa o indirectamente por un experto en el fenómeno y en la region de estudio. El proceso está basado en la experiencia individual y en el uso del razonamiento lógico. Las reglas de decisión son por lo tanto dificiles de formular por su complejidad y por que varían de lugar a lugar.

En estos métodos el experto puede decidir las variables y clases en que subdivide cada variable, y sobre todo el peso de las clases y el peso de las variables. De tal forma que obtiene una ecuación de susceptibilidad tal como :

\( S^n = W_1 w_c + W_2 w_c + W_3 w_c + W_n w_c \)

donde \(S^n\) es el valor de susceptibilidad de la celda n, \(W_i\) es el peso de la variable i y \(w_c\) es el peso de la clase a la cual pertenece la celda n en cada variable.

Los criterios utilizados generalmente por el experto son evidencia de actividad reciente, ambiente geomorfológico de cada unidad identificada, tipo de material y sus condiciones geomecánicas, pendiente de las laderas, relación con las unidades adyacentes, entre otros.

Entre las ventajas que se destacan de los métodos heurísticos está el papel dominante de la opinión del experto en el análisis, que puede ser un método utilizado en teoría a cualquier escala, sin embargo no son muy usados en escalas de detalle. También se destacan como ventaja que puede permitir una zonificación rápida incluyendo una gran cantidad de variables, y finalmente que cada poligono o unidad de análisis individual puede ser evaluado separadamente de acuerdo con su conjunto de condiciones únicas.

Como desventajas de estos métodos se señala que es una metodología subjetiva, ya que depende de la habilidad y experiencia del experto. Que sea subjetiva no es realmente una desventaja, el problema radica en la replicabilidad del método. Los análisis no se pueden generalizar y son propios en cada región. Esto mas que una desventaja es una realidad. Finalmente, se destaca que los resultados de estas metodologías son cualitativas, aunque algunas de estas metodologías utilice valoración cuantitativa estos valores son asignados subjetivamente.

Tipos de análisis heurísticos

Existen diferentes tipos de análisis heuristicos en cartografía geotécnica que se agrupan en métodos de mapeo directos, los cuales asignan el valor de susceptibilidad directamente en campo, y mapeo indirectos, que asignan dicho valor a las clases y/o variables y posteriormente se calcula la suscpetibilidad.

• Análisis geomorfológico (directo)

• Análisis basado en índices (indirecto)

• Análisis de decisión multicriterio (indirecto)

Análisis geomorfológico

Estos mapas corresponden a mapas geomorfológicos de procedimiento específico denominados mapas geomorfológicos pragmáticos (). En la construcción de estos mapas se debe realizar un análisis de terrenos donde inicialmente se reconocen varios atributos del terreno y se calasifican en unidades, subunidades y nivel de detalle de acuerdo con la escal del estudio. Los atributos utilizados en este ultimo nivel de detalle deben ser importantes para el alcance de la amenaza, en este caso atributos como la pendiente, el relieve, entre otros puede ser fundamental. Finalmente los terrenos clasificados deben ser evaluados en términos de susceptibilidad y/o amenaza de acuerdo con el análisis realizado.

Fig. 41 Mapa geomorfológico de amenaza. Tomado de Barredo et al., (2000)

Dentro de esta categoría se pueden incluir los mapas de zonificación geológico-geotécnica ampliamente utilizada en la decada de los 90´s en nuestra región. Entre estos se destaca la clasificación propuesta por el prof. Chica [1989] donde define las siguiente zonas:

• Subzonas tipo A – Estable independiente: su estabilidad es de alto grado pues sus condiciones naturales son favorables. Posiblemente llegaría a depender del manejo mismo que se le dé al terreno.

• Subzonas tipo B – Estable dependiente: su estabilidad depende de factores externos, los cuales se deben corregir. También de factores internos que implican un manejo determinado del terreno y cierto tipo de obras civiles que garanticen el no deterioro de esta estabilidad natural inicial.

• Subzonas tipo C – Inestable recuperable: la estabilidad de estos terrenos es critica o presenta inestabilidad manifiesta; sin embargo, con algunos correctivos específicos se puede mejorar la estabilidad, y en consecuencia, adelantar ciertas obras civiles en si interior.

• Subzonas tipo D – Inestable no recuperable: terrenos con inestabilidad manifiesta cuya recuperación no es posible o demasiado costosa comparada con las inversiones y tipo de obras proyectadas.

• Subzonas tipo E – Estable no utilizable: terrenos estables pero restringidos por condiciones urbanísticas u otras como estar ubicadas en vegas potenciales de inundación o cerca de frentes libres de taludes desprotegidos.

• Subzonas tipo F – Inestables no utilizables: terrenos inestables y restringidos por condiciones como las mencionadas para la zubzona anterior.

Fig. 42 Zonificación geológico-geotécnica del municipio de Yumbo (Valle). Tomado de Martinez et al., (1998)

Existen otras porpuestas como las de Aristizabal and Hermelin [2011]:

Fig. 43 Zonificación para la aptitud geotécnica del suelo propuesta por Aristizabal and Hermelin [2011].

Análisis basado en índices

Los mapas basados en índices combinan mapa de factores asociados con la ocurrencia de mvomientos en masa. Los pesos son determinados para cada factor basado en un estimativo de la influencia relativa de los movimientos en masa. Las variables son generalmente divididas en clases, los cuales son ponderados utilizando el criterio de expertos. Finalmente un índice de susceptibilidad es obtenido para cada unidad.

El metodo mas utilizado generalmente es un promedio de las clases a la que pertenece cada celda ponderado por el peso de cada variable.

Fig. 44 Ejemplo de combinación lineal ponderada. Tomado de Perez et al., (2005).

Análisis de decisión multicriterio

Se define como el conjunto de aproximaciones, métodos, modelos, técnicas y herramientas dirigidas a mejorar a calidad integral de los procesos de decisión seguidos por los individuos y los sistemas, para mejorar la efectividad, eficacia y eficiencia de los proceso de decisión y a incrementar el conocimiento de los mismos. Se basa en el paradigma de la Racionalidad como una aproximación orientada al proceso, cuyo propósito es la comprensión y el consenso. Y pretende la incorporación a los modelos de aspectos subjetivos, intangibles y no considerados, que condicionan la toma de decisiones de los individuos y organizaciones (Moreno (2000)).

Probablemente el método mas utilizado para movimientos en masa de este tipo se denomina Análisis Jerarquico de Procesos (AHP por sus siglas en inglés). Fue desarrollado por Saaty en la decada de los 60. El AHP utiliza comparaciones entre pares de elementos, construyendo una matriz a partir de estas comparaciones, que mide el juicio del tomador de decisiones de la importancia concerniente a cada criterio, agregando homogeneidad y cierto grado de certeza. Es una técnica multi-objetivo y multi-criteria para toma de decisiones que permite al usuario llegar a una escala de preferencias a partir de un determinado número de alternativas. Consiste en organizar una serie de factores en orden de jerarquía, asignando valores numéricos a valoraciones subjetivas sobre la relativa importancia de cada factor. Los pesos son obtenidos generalmente a través de los valores y vectores propios de la matriz. El vector propio que corresponde al mayor valor propio genera la prioridad relativa de los factores. También puede ser obtenido normalizando cada columna de la matriz de comparación, y calculando el promedio de las filas para resolver la matriz.

La escala utilizada en las comparaciones fue diseñada por Saaty. Esta escala incorporar los juicios o valoraciones del decisor. La escala es estrictamente positiva y elimina las ambigüedades que tiene el ser humano en comparar elementos en la proximidad del cero o del infinito. Los individuos son mas preciso al comparar elementos de la misma magnitud, número mágico de Miller –> 7(+/-2).

Fig. 45 Escala de Saaty.

Para evaluar la consistencia del análisis se estima el Radio de Consistencia (CR) de la siguiente forma:

\(CR=\frac{CI}{ICA}\)

Donde el CI es el Indice de Consistencia del análisis evaluado de la siguiente forma:

\(\frac{\lambda_{max}-n}{n-1}\)

Donde \(\lambda_{max}\) es el valor propio máximo de la matriz, \(n\) es el orden de la matriz. y el ICA se refiere al índice de consistencia aleatorio que se obtiene de la siguiente tabla de acuerdo con el \(n\):

Fig. 46 Indice de consistencia aleatoria.

El Radio de Consistencia debe ser <0.1

Fig. 47 Ejemplo de la aplicación del método de AHP para movimientos en masa tomado de Ayalew and Yamagishi [2004].

En algunos casos se combinan los métodos, es decir con un método se pueden asignar pesos a las clases, y con otro método peso a las variables. Un ejemplo se presenta en la siguiente figura donde AHP se utiliza para asignar pesos a las variables y el método de asignación directa es utilizada para asignar pesos a las clases:

Fig. 48 Ejemplo de combinación de métodos.

Python

AHP

A continuación se describe el procedimiento para implmentar el método de AHP con Python. El ejercicio parte con la matriz de comparación de la Figura del ejemplo de Ayalew and Yamagishi, denominada A. Para definir los pesos de las varables con el método AHP, se puede utilizar la función linalg.eig que obtiene los valores y vectores propios. Es importante tener en cuenta que los vectores propios generados por Python están normalizados euclidianamente, por lo tanto hay que normalizarlos a la unidad (1) con la funcion norm.

import numpy as np

A=([[1, 0.33,  0.33,  1, 0.33, 0.33],
    [3,    1,  0.33,  5,    1,    1],
    [3,    3,     1,  3,    1,    1],
    [1,  0.2,  0.33,  1,    1,  0.2],
    [3,    1,     1,  1,    1, 0.33],
    [3,    1,     1,  5,    3,    1]])

B=np.array(A) # para transformarla en una matriz

values, vectores=np.linalg.eig(B) # Función para calcular los valores y vectores propios

vector_norm=vectores/np.linalg.norm(vectores, ord=1) # normalización de los vectores

print('esto son los valores propios',values)

esto son los valores propios [ 6.45135611+0.j         -0.0241081 +1.64871645j -0.0241081 -1.64871645j
 -0.13454859+0.43520127j -0.13454859-0.43520127j -0.13404274+0.j        ]

print('esto son los vectores propios', vectores)

esto son los vectores propios [[ 0.14436866+0.j          0.02398294+0.00827384j  0.02398294-0.00827384j
   0.20536727+0.14878211j  0.20536727-0.14878211j  0.14221686+0.j        ]
 [ 0.42599629+0.j          0.01147632+0.48741276j  0.01147632-0.48741276j
   0.1945605 -0.27358166j  0.1945605 +0.27358166j  0.0758326 +0.j        ]
 [ 0.56812531+0.j          0.66446338+0.j          0.66446338-0.j
  -0.78171181+0.j         -0.78171181-0.j         -0.71758058+0.j        ]
 [ 0.1578558 +0.j         -0.15986003-0.05675779j -0.15986003+0.05675779j
  -0.07345944-0.04273917j -0.07345944+0.04273917j -0.21773253+0.j        ]
 [ 0.32625087+0.j          0.09149542-0.33367399j  0.09149542+0.33367399j
   0.16766496-0.13753574j  0.16766496+0.13753574j  0.2047162 +0.j        ]
 [ 0.58614025+0.j         -0.39877545+0.11239927j -0.39877545-0.11239927j
  -0.26017993+0.29994993j -0.26017993-0.29994993j  0.60810009+0.j        ]]

print('esto son los vectores propios normalizados',vector_norm)

esto son los vectores propios normalizados [[ 0.06536254+0.j          0.01085821+0.00374596j  0.01085821-0.00374596j
   0.0929795 +0.06736071j  0.0929795 -0.06736071j  0.06438831+0.j        ]
 [ 0.19286871+0.j          0.00519587+0.22067486j  0.00519587-0.22067486j
   0.08808676-0.12386338j  0.08808676+0.12386338j  0.03433301+0.j        ]
 [ 0.25721725+0.j          0.30083406+0.j          0.30083406-0.j
  -0.35391798+0.j         -0.35391798+0.j         -0.32488273+0.j        ]
 [ 0.0714688 +0.j         -0.07237621-0.02569694j -0.07237621+0.02569694j
  -0.03325857-0.01935005j -0.03325857+0.01935005j -0.09857784+0.j        ]
 [ 0.14770923+0.j          0.04142431-0.15107003j  0.04142431+0.15107003j
   0.07590987-0.06226895j  0.07590987+0.06226895j  0.09268472+0.j        ]
 [ 0.26537347+0.j         -0.18054454+0.05088847j -0.18054454-0.05088847j
  -0.11779579+0.13580155j -0.11779579-0.13580155j  0.27531573+0.j        ]]

Los anteriores valores corresponden a los valores propios de la matriz. Se obtiene entonces el vector propio del mayor valor propio, en ese caso corresponde al primer valor propio.

w=vector_norm[:,0]
print(w)

[0.06536254+0.j 0.19286871+0.j 0.25721725+0.j 0.0714688 +0.j
 0.14770923+0.j 0.26537347+0.j]

Estos valores significan que la primera variable Aspect tiene un peso del 6%, la segunda variable Elevation del 19%, la tercera variable Lithology del 25%, la cuarta variable Plan curvature del 7%, la quinta variable Profile curvature del 14%, y la sexta variable Slope gradient del 26%.

Para calcular la consistencia del análisis se procede entonces a calcular el indice de consistencia, con \(\lambda_{max}\) que representa el valor propio máximo, n que corresponde a la longitud de la matrix, y el índice de consistencia aleatorio que se obtiene de la tabla en la Figura.

CI=(values[0]-len(values))/(len(values)-1)

CR= CI/1.24

print(CR)

(0.07279937283948756+0j)

Se obtiene un radio de consistencia \(0.07<0.1\) por lo tanto el análisis esta OK.

Método combinado

En este caso se evaluará la susceptibilidad por movimientos en masa en la cuenca de la quebrada La Miel en el municipio de Caldas (Antioquia). Se utilizará el ejemplo anterior, donde se asignaron pesos a las clases, y se combinará con asignación directa de pesos a las clases que conforman cada variable.

Se procede entonces a importar cada uno de los mapas a utilizar. En este caso 6 mapas de las variables predictoras que se utilizaron en el método AHP.

!pip install rasterio

Requirement already satisfied: rasterio in c:\users\edier\miniconda3\lib\site-packages (1.3.9)
Requirement already satisfied: affine in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (2.4.0)
Requirement already satisfied: attrs in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (24.2.0)
Requirement already satisfied: certifi in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (2023.11.17)
Requirement already satisfied: click>=4.0 in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (8.1.6)
Requirement already satisfied: cligj>=0.5 in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (0.7.2)
Requirement already satisfied: numpy in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (1.25.1)
Requirement already satisfied: snuggs>=1.4.1 in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (1.4.7)
Requirement already satisfied: click-plugins in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (1.1.1)
Requirement already satisfied: setuptools in c:\users\edier\miniconda3\lib\site-packages (from rasterio) (67.8.0)
Requirement already satisfied: colorama in c:\users\edier\miniconda3\lib\site-packages (from click>=4.0->rasterio) (0.4.6)
Requirement already satisfied: pyparsing>=2.1.6 in c:\users\edier\miniconda3\lib\site-packages (from snuggs>=1.4.1->rasterio) (3.0.9)

import rasterio as rio
import matplotlib.pyplot as plt
import numpy as np

raster = rio.open('https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/Pendiente.tif?raw=true')
pendiente=raster.read(1)
pendiente=np.where(pendiente<0,np.nan,pendiente)
plt.imshow(pendiente);
plt.colorbar();

---------------------------------------------------------------------------
CPLE_HttpResponseError                    Traceback (most recent call last)
File rasterio\\_base.pyx:310, in rasterio._base.DatasetBase.__init__()

File rasterio\\_base.pyx:221, in rasterio._base.open_dataset()

File rasterio\\_err.pyx:221, in rasterio._err.exc_wrap_pointer()

CPLE_HttpResponseError: HTTP response code: 404

During handling of the above exception, another exception occurred:

RasterioIOError                           Traceback (most recent call last)
Cell In[8], line 1
----> 1 raster = rio.open('https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/Pendiente.tif?raw=true')
      2 pendiente=raster.read(1)
      3 pendiente=np.where(pendiente<0,np.nan,pendiente)

File ~\miniconda3\Lib\site-packages\rasterio\env.py:451, in ensure_env_with_credentials.<locals>.wrapper(*args, **kwds)
    448     session = DummySession()
    450 with env_ctor(session=session):
--> 451     return f(*args, **kwds)

File ~\miniconda3\Lib\site-packages\rasterio\__init__.py:317, in open(fp, mode, driver, width, height, count, crs, transform, dtype, nodata, sharing, **kwargs)
    314 path = _parse_path(raw_dataset_path)
    316 if mode == "r":
--> 317     dataset = DatasetReader(path, driver=driver, sharing=sharing, **kwargs)
    318 elif mode == "r+":
    319     dataset = get_writer_for_path(path, driver=driver)(
    320         path, mode, driver=driver, sharing=sharing, **kwargs
    321     )

File rasterio\\_base.pyx:312, in rasterio._base.DatasetBase.__init__()

RasterioIOError: HTTP response code: 404

De acuerdo con el método estos mapas se deben reclasificar en clases y pesos con criterio de experto. Se recomienda utilizar los rangos recomendados por el SGC o por referencias conocidas. Este ejercicio simplemente señala el procedimiento, pero no tiene ningún análisis o criterio la reclasificación utilizada. Para este caso se utilizarán valores a las clases en un rango de 0 a 1. Donde 0 significa baja incidencia en la ocurrencia de movimientos en masa y 1 significa muy alta.

El procedimiento entonces corresponde a reclasificar en clases cada mapa y asignar un valor entre 0 a 1 a clada clase.

pendiente_re=np.where ( (np.logical_and (pendiente>=0, pendiente<10 )),0.1,pendiente );
pendiente_re=np.where ( (np.logical_and (pendiente_re>=10, pendiente_re<30 )),0.5,pendiente_re);
pendiente_re=np.where ( pendiente_re>=30,1,pendiente_re);
print(np.unique(pendiente_re));
plt.imshow(pendiente_re);
plt.colorbar();

[0.1 0.5 1.  nan]

raster = rio.open('https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/Geologia_Superficial.tif?raw=true')
geologia=raster.read(1)
geologia=np.where(geologia<0,np.nan,geologia)
print(np.unique(geologia));
plt.imshow(geologia);
plt.colorbar();

[ 2.  4.  6.  8.  9. 10. 11. 14. 15. 16. nan]

geologia_re=np.where ( geologia>=14,1,geologia)
geologia_re=np.where ( geologia_re==9,0.1,geologia_re)
geologia_re=np.where ( geologia_re==4,0.4,geologia_re)
geologia_re=np.where ( geologia_re>=2,0.2,geologia_re)
print(np.unique(geologia_re))
plt.imshow(geologia_re);
plt.colorbar();

[0.1 0.2 0.4 1.  nan]

raster = rio.open(r'https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/Aspecto.tif?raw=true')
aspecto=raster.read(1)
aspecto=np.where(aspecto<0,np.nan,aspecto)
plt.imshow(aspecto);
plt.colorbar();

aspecto_re=np.where ( aspecto<90,0.2,aspecto);
aspecto_re=np.where ( (np.logical_and (aspecto_re>=90, aspecto_re<180 )),0.5,aspecto_re);
aspecto_re=np.where ( (np.logical_and (aspecto_re>=180, aspecto_re<270 )),0.9,aspecto_re);
aspecto_re=np.where ( aspecto_re>=270,0.1,aspecto_re);
print(np.unique(aspecto_re))
plt.imshow(aspecto_re);
plt.colorbar();

[0.1 0.2 0.5 0.9 nan]

raster = rio.open('https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/DEM5m.tif?raw=true')
elevacion=raster.read(1)
elevacion=np.where(elevacion<0,np.nan,elevacion)
plt.imshow(elevacion);
plt.colorbar();

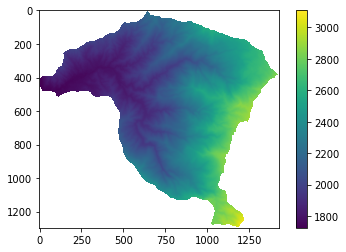
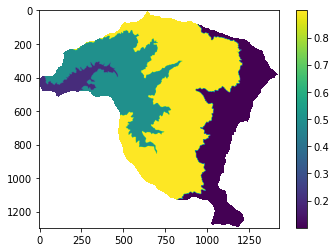
elevacion_re=np.where ( elevacion<1800,0.2,elevacion);
elevacion_re=np.where ( (np.logical_and (elevacion_re>=1800, elevacion_re<2000 )),0.5,elevacion_re);
elevacion_re=np.where ( (np.logical_and (elevacion_re>=2000, elevacion_re<2500 )),0.9,elevacion_re);
elevacion_re=np.where ( elevacion_re>=2500,0.1,elevacion_re);
print(np.unique(elevacion_re))
plt.imshow(elevacion_re);
plt.colorbar();

[0.1 0.2 0.5 0.9 nan]

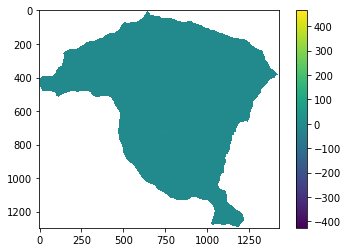
raster = rio.open('https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/CurvaturaPerfil.tif?raw=true')
curvaturaV=raster.read(1)
curvaturaV=np.where(curvaturaV==-999.0,np.nan,curvaturaV) # en este caso no se puede utilizar <0 por que hay valores de curvatura que son negativos
plt.imshow(curvaturaV);
plt.colorbar();

curvaturaV_re=np.where ( curvaturaV>=0.005,0.9,curvaturaV);
curvaturaV_re=np.where ( (np.logical_and (curvaturaV_re>=-0.5, curvaturaV_re<0.5 )),0.1,curvaturaV_re);
curvaturaV_re=np.where ( curvaturaV_re<-0.005,0.3,curvaturaV_re);
print(np.unique(curvaturaV_re))
plt.imshow(curvaturaV_re);
plt.colorbar();

[0.1 0.3 0.9 nan]

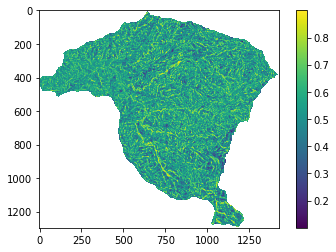
raster = rio.open('https://github.com/edieraristizabal/Libro_cartoGeotecnia/blob/master/data/CurvaturaPlana.tif?raw=true')
curvaturaH=raster.read(1)
curvaturaH=np.where(curvaturaH==-999.0,np.nan,curvaturaH) # en este caso no se puede utilizar <0 por que hay valores de curvatura que son negativos
plt.imshow(curvaturaH);
plt.colorbar();

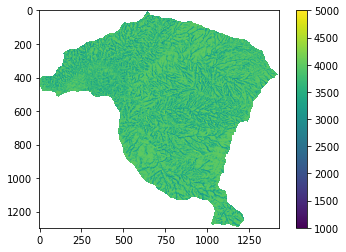
curvaturaH_re=np.where ( curvaturaH<=2000,0.9,curvaturaH);
curvaturaH_re=np.where ( (np.logical_and (curvaturaH_re>=2000, curvaturaH_re<=3000 )),0.1,curvaturaH_re);
curvaturaH_re=np.where ( curvaturaH_re>3000,0.1,curvaturaH_re);
print(np.unique(curvaturaH_re))
plt.imshow(curvaturaH_re);
plt.colorbar();

[0.1 0.9 nan]

print(w[0],w[1],w[2],w[3],w[4],w[5])

(0.06536253617532849+0j) (0.1928687090376127+0j) (0.2572172528769481+0j) (0.07146880296600812+0j) (0.14770923077095524+0j) (0.2653734681731474+0j)

Finalmente se aplica la ecuacion de IS y se obtiene el mapa.

IS=0.065*aspecto_re+0.192*elevacion_re+0.257*geologia_re+0.071*curvaturaH_re+0.147*curvaturaV_re+0.265*pendiente_re
plt.imshow(IS);
plt.colorbar();

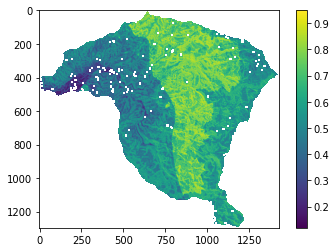
Para exportar el mapa como archivo tiff y poder trabajar en un GIS, se puede utilizar la libreria rasterio, y sustraer los datos de georeferenciacion y tamaño del mapa de aspecto en ese caso.

meta=raster.profile
raster_transform = meta['transform']
raster_crs = meta['crs']

with rio.open('IS.TIF', 'w', 
              driver='Gtiff',height=aspecto.shape[0],width=aspecto.shape[1],count=1,
              dtype='float64',nodata=-999,crs=raster_crs,transform=raster_transform) as dst:
    dst.write(IS,1);

Referencias

1(1,2)

Edier Aristizabal and Michel Hermelin. Propuesta de zonificación del suelo para la gestión del riesgo enfocada al ordenamiento territorial. Gestión y Medio Ambiente, 14:7–16, 2011.

2

Lulseged Ayalew and Hiromitsu Yamagishi. Slope failures in the blue nile basin, as seen from landscape evolution perspective. Geomorphology, 57:95–116, 2004. doi:10.1016/S0169-555X(03)00085-0.

3

Alejandro Chica. Apuntes de geotecnia. cursos de geotecnia y prácticas geotécnicas, Facultad Nacional de Minas, :, 1989.