
ANÁLISIS GEOESPACIAL
Prof. Edier Aristizábal

First Law of Geography
“Everything is related to everything else, but near things are more related than distant things."
Waldo R. Tobler (1970)
Second Law of Geography
“Geographic variables exhibit uncontrolled variance."
Goodchild (2004)
Introducción
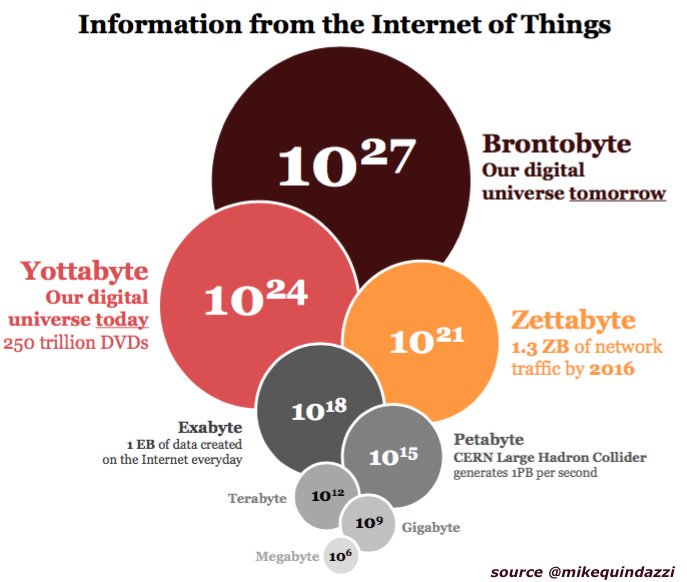
La era de los datos
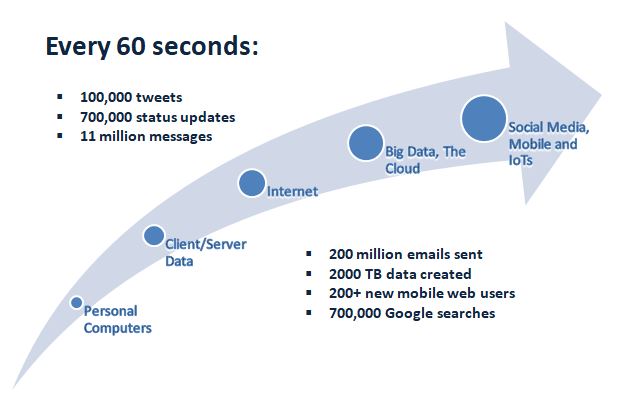
Data store

Data store
Los kilobytes eran almacenados en discos, megabytes fueron almacenados en discos duros, terabytes fueron almacenados en arreglos de discos, y petabytes son almacenados en la nube.

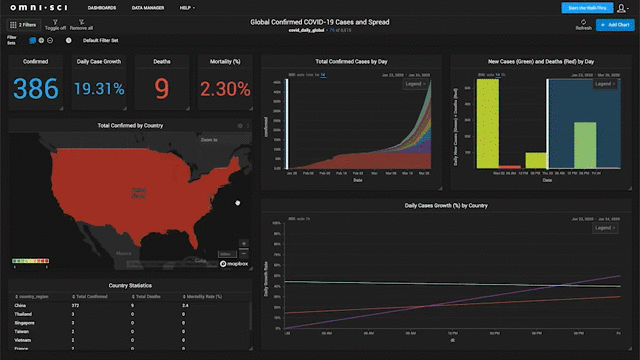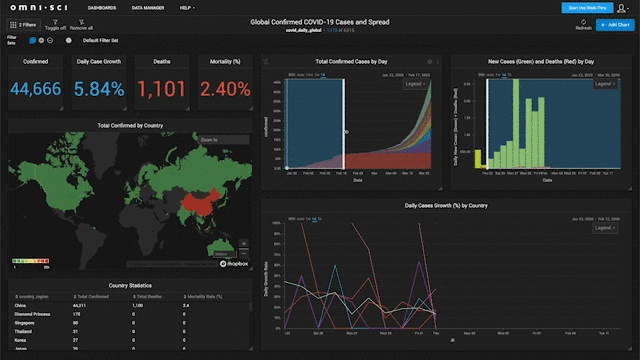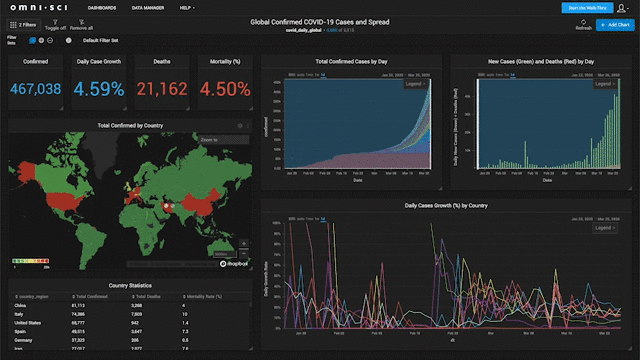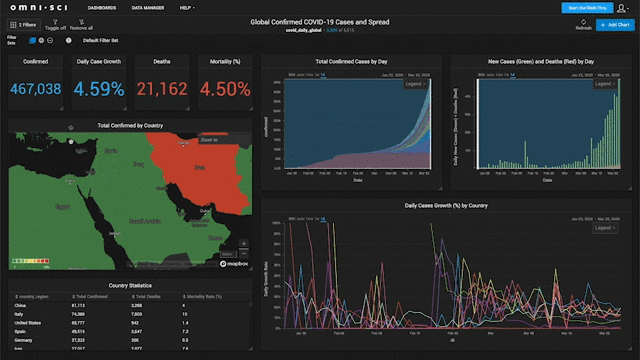
Why spatial is special?

Why spatial is special?

Why spatial is special?
Why spatial is special?
Charles Picquet (1832)

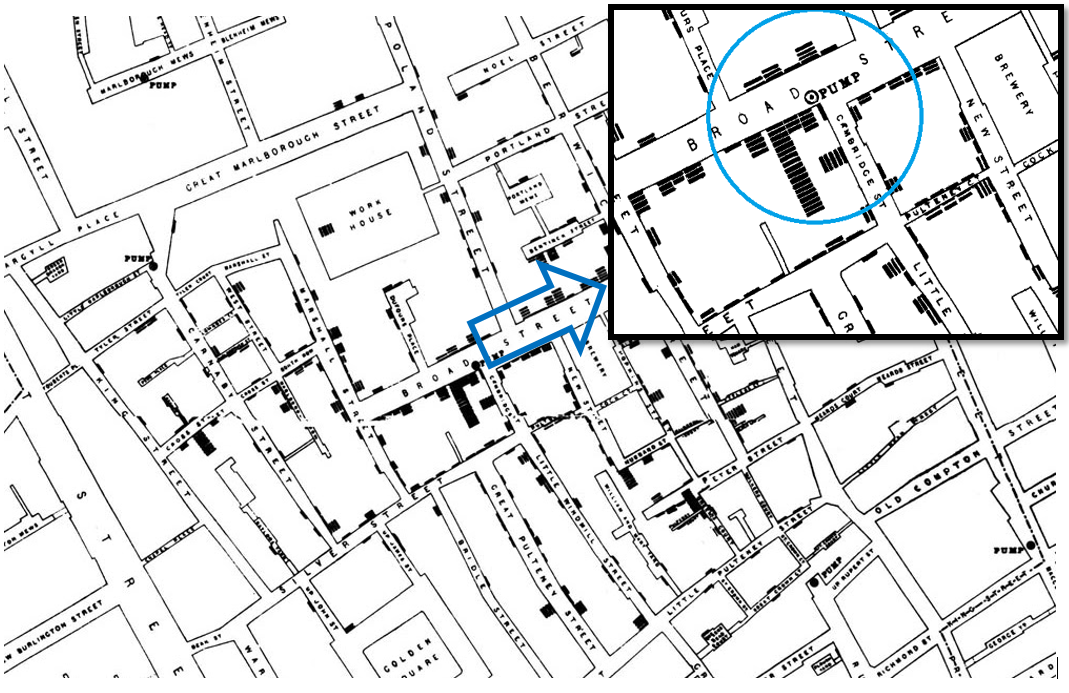
Dr. John Snow (1854)
Fotografía aérea (1858)

Remote sensing (1972)

Roger F. Tomlinson (1960)

Actualidad

Actualidad

Actualidad
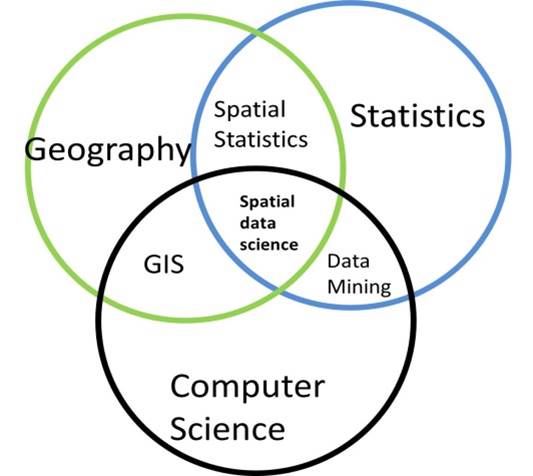
Geospatial Data Science
Geospatial data science (GDS) is a subset of Data Science that focuses on the unique characteristics of spatial data, moving beyond simply looking at where things happen to understand why they happen there
The extraction of meaningful information from data involving location, geographic proximity and/or spatial interaction through the use techniques specifically designed to deal appropriately with spatial data.
Spatial data science is an interdisciplinary field that focuses on analyzing and interpreting data that has a geographic or spatial component. Spatial data science works with data that is tied to a specific location on the Earth’s surface.
Spatial analysis
- Spatial data manipulation through geographical information systems (GIS),
- Spatial data analysis in a descriptive and exploratory way (Python, JS, R...),
- Spatial statistics that employ statistical procedures to investigate if inferences can be made
- Spatial modeling which involves the construction of models to identify relationships and predict outcomes in a spatial context.
Spatial analysis
Spatial data science merges several areas, including:
- Geospatial Analysis: The study and interpretation of geographic data through spatial algorithms.
- Machine Learning: The use of statistical models and machine learning algorithms to make predictions or discover patterns in geospatial data.
- Data Visualization: Creating maps, charts, and other visualizations that represent the spatial distribution of data.
- Spatial Statistics: Applying statistical techniques to understand spatial patterns and relationships.
Spatial analysis

Herramientas
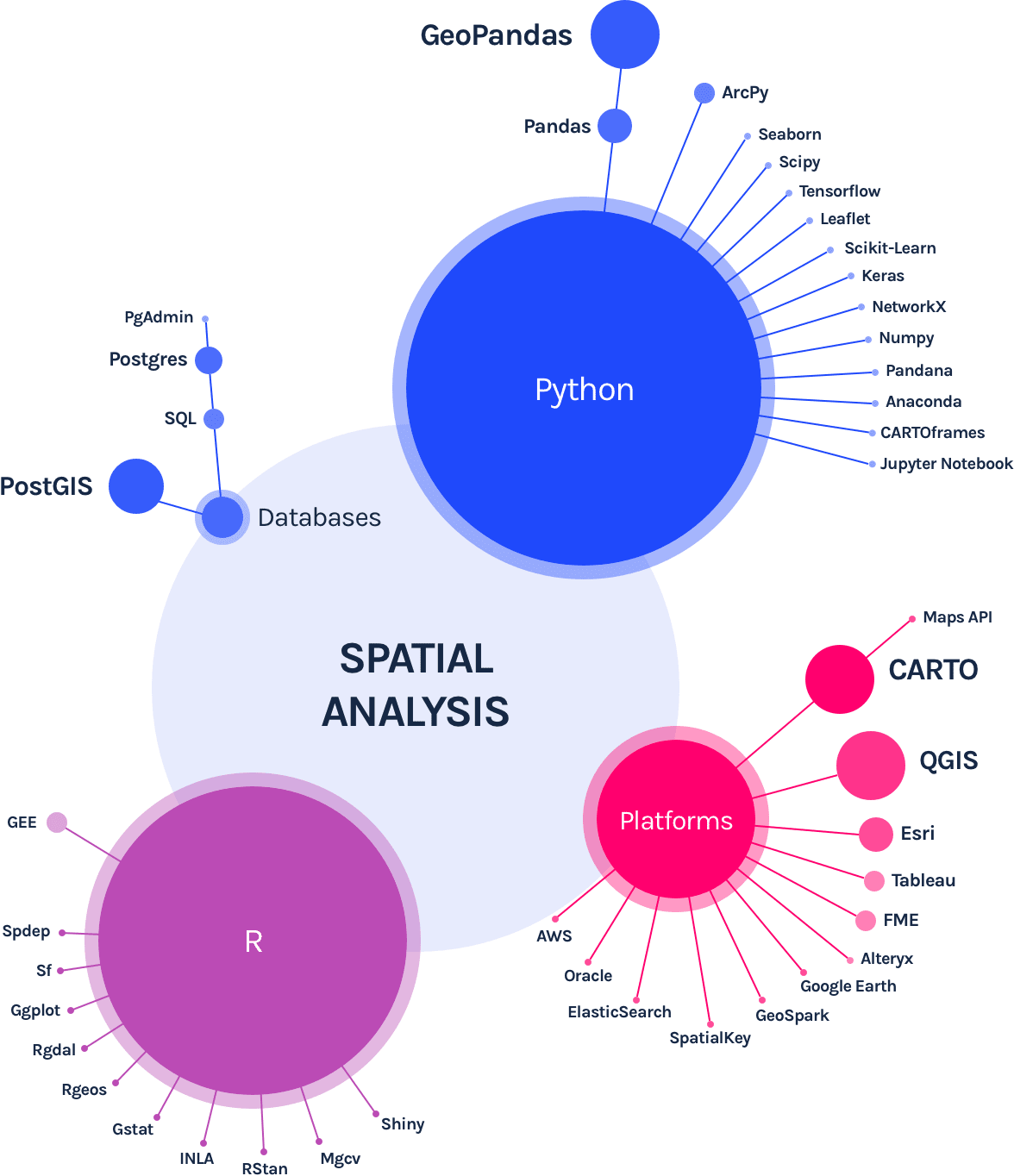
https://carto.com/what-is-spatial-data-science/
Ambiente de trabajo
TIOBE index - Programming languaje popularity

Python
Python code is fast to develop: As the code is not required to be compiled and built, Python code can be much readily changed and executed. This makes for a fast development cycle.
Python code is not as fast in execution: Python code runs a little slow as compared to conventional languages like C, C++, etc.
Python is interpreted: Python does not need compilation to binary code, which makes Python easier to work with and much more portable than other programming languages.
Python is object oriented: Many modern programming languages support object-oriented programming. ArcGIS and QGIS is designed to work with object-oriented languages, and Python qualifies in this respect.
Paquetes

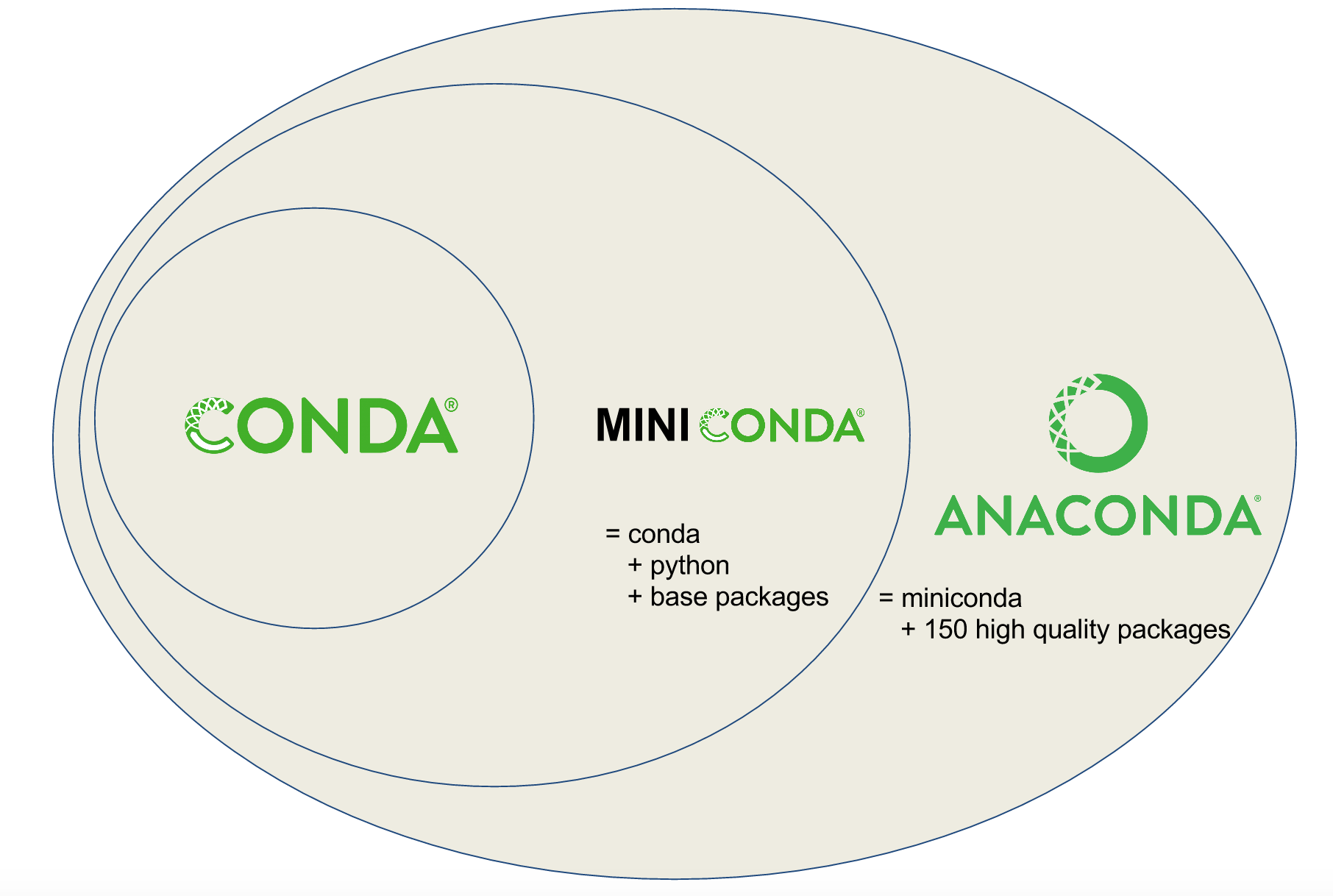
Conda
PIP

Docker

R

RStudio

Javascript

Google Earth Engine

Material de apoyo
Thinking spatial
Fenómenos espaciales
La suposición estadística de independencia e idéntica distribución (iid) es equivalente a asumir datos homogéneos. En otras palabras, la media y la varianza de una variable aleatoria son constantes entre las observaciones, al igual que todos los demás momentos (asimetría y curtosis).
La pregunta a abordar es sí la media y la varianza de algún fenómeno varían o no entre las regiones en las que se divide un paisaje?
Spatial dependence
La dependencia espacial implica que las observaciones en una región están correlacionadas con las de las regiones vecinas (Fletcher, 2018). La dependencia espacial se mide frecuentemente mediante la covarianza y, por lo tanto, es una propiedad de segundo orden - covarianza.
Spatial heterogeneity
la heterogeneidad espacial se refiere a los efectos del espacio sobre las unidades muestrales, en las cuales la media varía de un lugar a otro (Zhang, 2023). Por lo tanto, la heterogeneidad espacial es una propiedad de primer orden - la media (Wang, 2022)
Tipos de análisis espaciales
- Análisis de patrones de puntos: modelado de eventos en un dominio (D) aleatorio. En el análisis de patrones de puntos, el enfoque es diferente porque aquí se trata de estudiar la distribución de eventos puntuales en el espacio, y dichos puntos (que representan eventos u ocurrencias) son considerados como realizaciones de un proceso estocástico.
- Análisis de datos areales o discretos (lattice): modelado donde el dominio (D) de los datos espaciales es discreto y fijo, donde las regiones espaciales que definen el dominio pueden tener formas regulares (grid o píxeles) o formas irregulares (polígonos).
- Análisis geoestadístico: modelado donde el dominio (D) de los datos espaciales es una superficie continua (campos) y fija. En geoestadística como en análisis de datos discretos, el atributo no es lo que define si los datos son espacialmente continuos o discretos; en este caso la continuidad proviene del hecho de que el dominio (D) permite realizar mediciones en cualquier lugar.
Scale
Scale is also important because it can inform about sampling for training experience. Learning is more reliable when the distribution of the samples in the training experience is similar to the distribution of the test experience. In many geographic studies, training occurs on data from a specific geographic area. This makes it challenging to use the trained model for other geographic regions because the distribution of the test and train data sets is not similar, due to spatial heterogeneity.
This means that the sampling strategy for the training data set is essential to cover the heterogeneity of the phenomena of interest over the spatial frame of study. By increasing the extent of the study area, more processes and contextual environmental factors may alter the variable and result in non-stationarity by interweaving spatial patterns of different scales or inconsistent effect of processes in different regions.
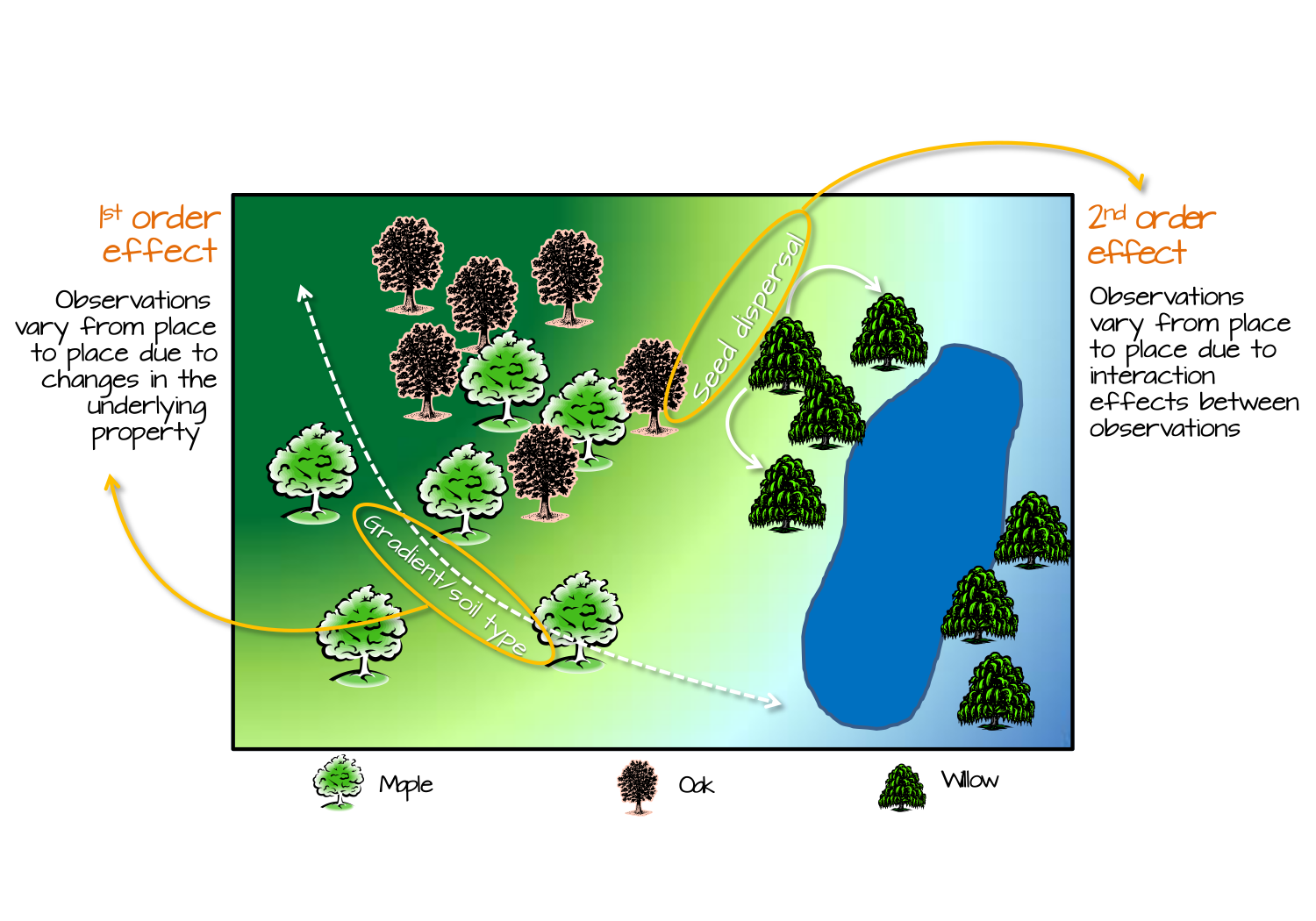
First and second order effects
Tree density distribution can be influenced by 1st order effects such as elevation gradient or spatial distribution of soil characteristics; and by 2nd order effects such as seed dispersal processes where the process is independent of location and, instead, dependent on the presence of other trees.
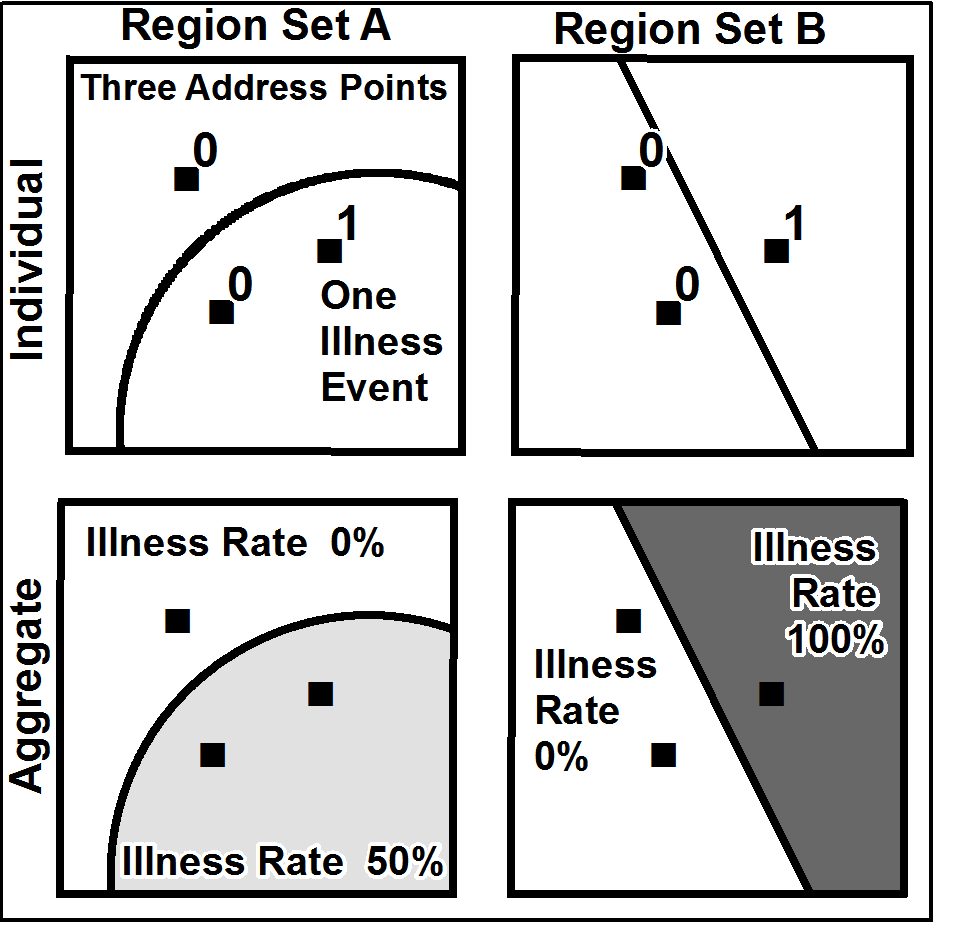
MAUP
The Modifiable Area Unit Problem (MAUP) problem refers to the influence the zone design has on the outcomes of the analysis. A different designation would probably lead to different results.
MAUP

MAUP
There are two types of biases for the MAUP:

Zonal effect
The zonal effect occurs when you group data by various artificial boundaries. In this type of MAUP error, each subsequent boundary yields major analytical differences.
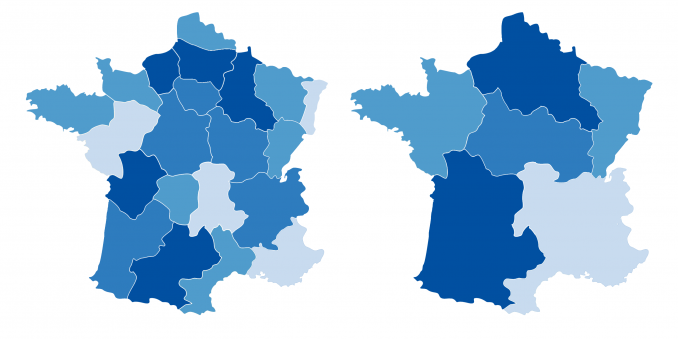
Scale effect
The scale effect occurs when maps show different analytical results at different levels of aggregation. Despite using the same points, each successive smaller unit consequently changes the pattern.
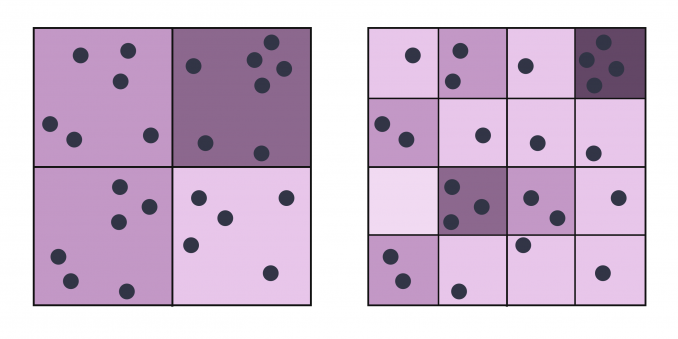


Edge effect

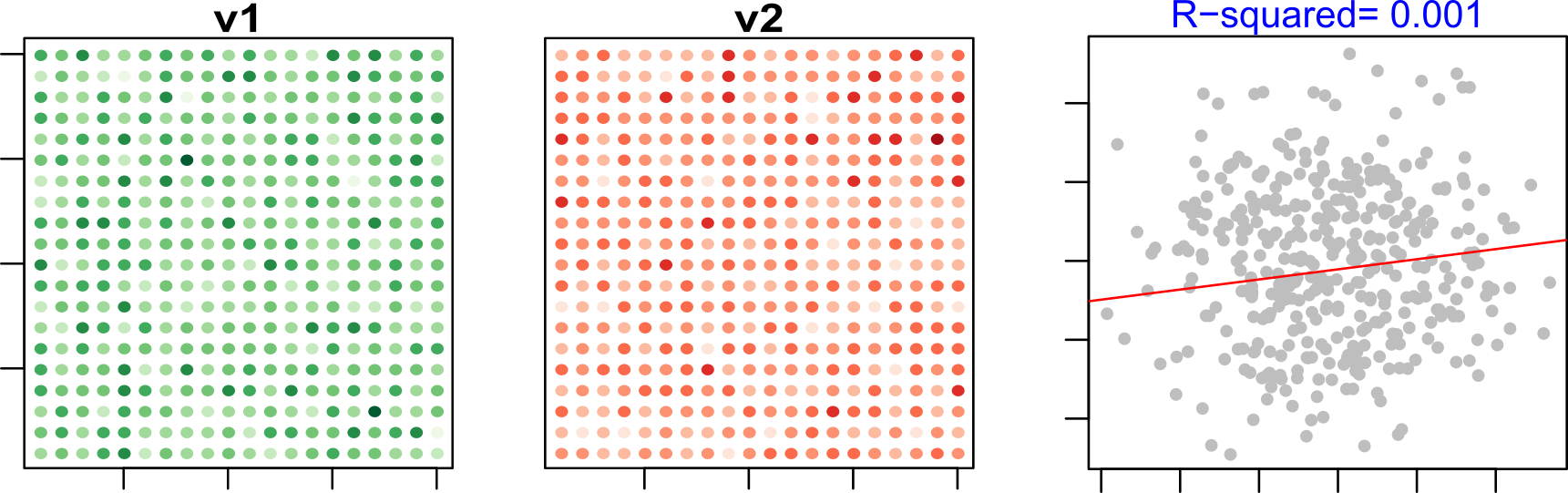
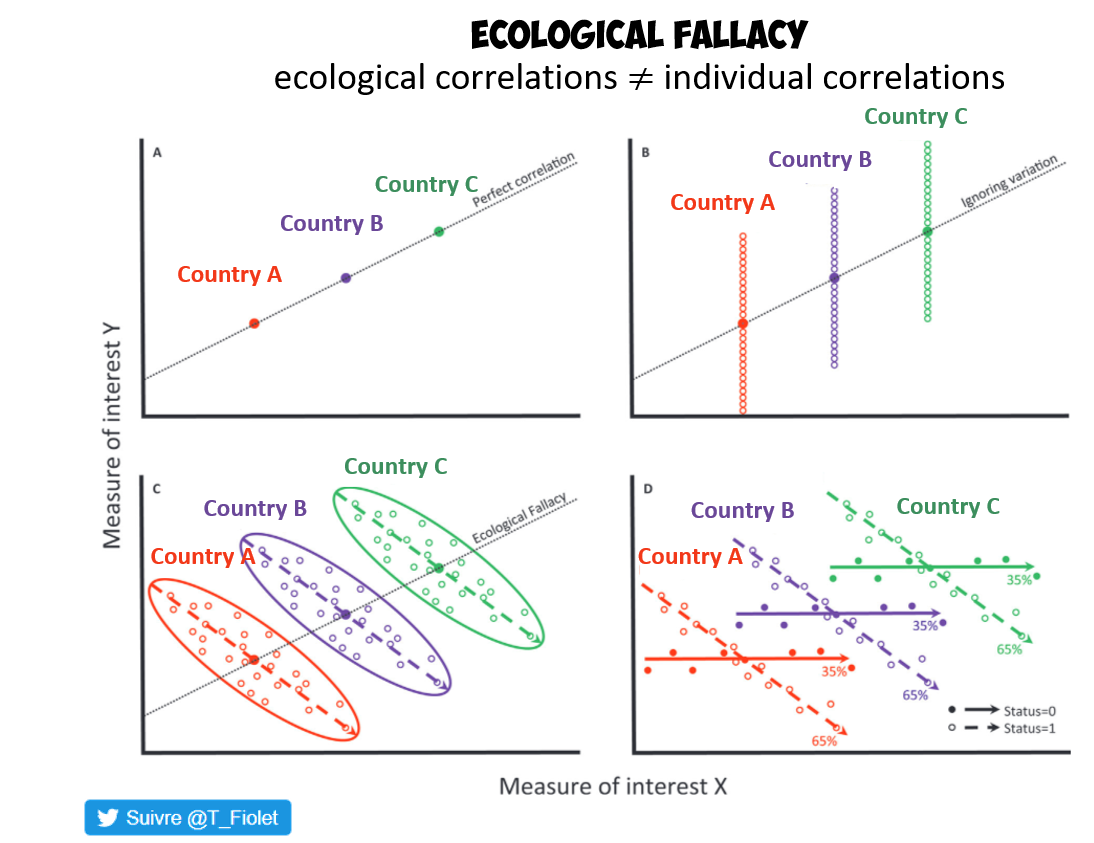
Ecological Fallacy
This problem occurs when a relationship that is statistically significant at one level of analysis is assumed to hold true at a more detailed level as well. This is a typical mistake that occurs when we use aggregated data to describe the behavior of individuals.

Neighborhood effect
The characteristics of neighboring properties might have certain impact on the same characteristic to neighbors.
Los efectos locales se refieren a patrones o relaciones espaciales que varían a nivel de una unidad espacial específica o en un vecindario pequeño.
Los efectos globales son los efectos que se suponen constantes a lo largo de todo el espacio.
Efectos de X sobre y
Los efectos directos son los efectos que una variable independiente tiene sobre la variable dependiente en la misma unidad espacial.
Los efectos indirectos son los efectos que una variable explicativa en una unidad tiene sobre la variable dependiente en otras unidades vecinas.
El término spillover es sinónimo de efectos indirectos, pero a veces se usa de forma más cualitativa para describir el fenómeno general de propagación del efecto entre unidades
Los efectos marginales son la derivada de la variable dependiente respecto a una variable explicativa.
Los efectos fijos (fixef effects) capturan características específicas y constantes de cada unidad. Se modelan como parámetros específicos para cada unidad.
Los efectos aleatorios (random effects) se usan en modelos jerarquicos para entender el patron general, se estiman como una varianza común que describe la variabilidad entre las unidades.
Efectos de X sobre y
| Tipo de efecto | ¿Qué representa? | ¿Depende de la estructura espacial? | ¿Unidad específica? |
|---|---|---|---|
| Directo | Efecto de X sobre Y en la misma unidad | ✅ | ✅ |
| Indirecto | Efecto de X sobre Y en unidades vecinas | ✅ | ❌ |
| Spillover | Propagación espacial de los efectos | ✅ | ❌ |
| Marginal | Cambio en Y ante un cambio unitario en X | ✅ (en modelos espaciales) | Depende |
| Fijo | Diferencias no observadas por unidad | ❌ (no espacial por defecto) | ✅ |
| Aleatorio | Variabilidad aleatoria entre unidades | ✅ (Modelos Jerárquicos) | ❌ |
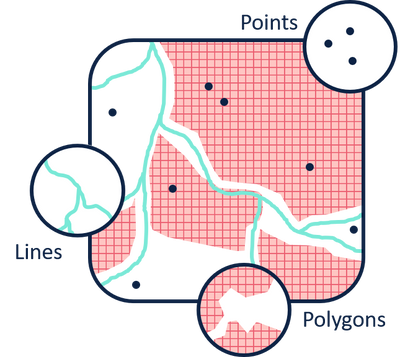
Spatial data
Data

Spatial data
Spatial data is geographically referenced data, given at known locations and often represented visually through maps. That geographic reference, or the location component of the data, may be represented using any number of coordinate reference systems, for example, longitude and latitude.
Geospatial data
Geospatial data is data about objects, events, or phenomena that have a location on the surface of the earth, including location information, attribute information (the characteristics of the object, event, or phenomena concerned), and often also temporal information (the time or life span at which the location and attributes exist)
Models are simplifications of reality

Spatial Data Models
- Data can be defined as verifiable facts about the real world.
- Information is data organized to reveal patterns, and to facilitate search.
- Data model: an abstraction of the real world which incoprorates only those properties thought to be relevant to the application
- Data structure: a representation of the data model
- File format: the representation of the data in storage hardware
Real world data must be described in terms of a data model, then a data structure must be chosen to represent the data model, and finally a file format must be selected that is suitable for that data structure.
Types of spatial models
- Object-based (feature) model: In the object view, we consider the world as a series of entities located in space. Entities are (usually) real. An object is a digital representation of all or part of an entity, which can be described in detail according to their boundary lines and other objects that constitute them or are related to them.
- Field model: In the field view, the world consists of properties continuously varying across space. It represents data that are considered to be continuously changing in two-dimensional or three-dimensional space. In a field, every location has a value (including ‘‘not here’’ or zero) and sets of values taken together define the field.
Data Structure

Object-based model
Vector
objects are frequently not as simple as this geometric view leads one to assume. They may exist in three spatial dimensions, move and change over time, have a representation that is strongly scale-dependent, relate to entities that are themselves fuzzy and/or have indeterminate boundaries, or even be fractal.
Vector (tabla geográfica)
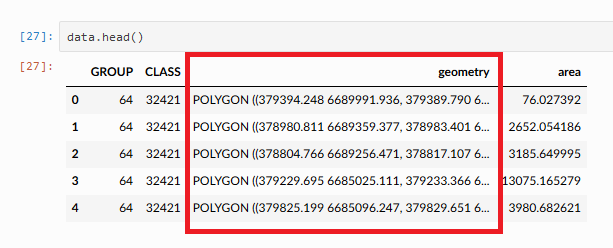
Shapefile
A shapefile is a file-based data format native to ArcView software . Conceptually, a shapefile is a feature class–it stores a collection of features that have the same geometry type (point, line, or polygon), the same attributes, and a common spatial extent. Despite what its name may imply, a “single” shapefile is actually composed of at least three files, and as many as eight. Each file that makes up a “shapefile” has a common filename but different extension type.
Arc-Info Interchange (e00)
An ArcInfo interchange file, is also known as an export file type, this file format is used to enable a coverage, grid or TIN, and an associated INFO table to be transferred between different machines. This file has the .e00 extension.
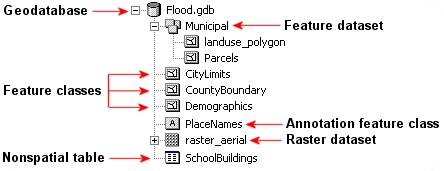
File Geodatabase
A file geodatabase is a relational database storage format. It’s a far more complex data structure than the shapefile and consists of a .gdb folder housing dozens of files. Its complexity renders it more versatile allowing it to store multiple feature classes and enabling topological definitions. An example of the contents of a geodatabase is shown in the following figure.
GeoPackage
This is a relatively new data format that follows open format standards (i.e. it is non-proprietary). It’s built on top of SQLite (a self-contained relational database). Its one big advantage over many other vector formats is its compactness–coordinate value, metadata, attribute table, projection information, etc…, are all stored in a single file which facilitates portability. Its filename usually ends in .gpkg. Applications such as QGIS (2.12 and up), R and ArcGIS will recognize this format (ArcGIS version 10.2.2 and above will read the file from ArcCatalog but requires a script to create a GeoPackage).
Geojson
GeoJSON is an Open Standard Format designed for representing simple geographical features, along with their non-spatial attribute
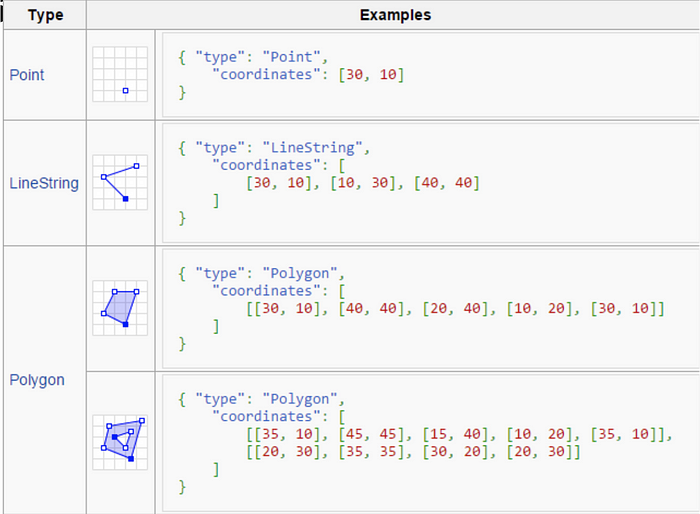
Geojson -- Multi-part geometry
Multi-part geometry types are similar to their single-part counterparts. The only difference is that one more hierarchical level is added into the coordinates array, for specifying multiple shapes.

Geojson -- Geometry collections
A geometry collection is a set of several geometries, where each geometry is one of the previously listed six types, i.e., any geometry type excluding "GeometryCollection". For example, a "GeometryCollection" consisting of two geometries, a "Point" and a "MultiLineString", can be defined as follows:

Geojson -- Feature
A "Feature" is formed when a geometry is combined with non-spatial attributes, to form a single object. The non-spatial attributes are encompassed in a property named "properties", containing one or more name-value pairs—one for each attribute. For example, the following "Feature" represents a geometry with two attributes, named "color" and "area":

Geojson -- Feature Collections
A "FeatureCollection" is, like the name suggests, a collection of "Feature" objects. The separate features are contained in an array, comprising the "features" property. For example, a "FeatureCollection" composed of four features can be specified as follows:

http://geojson.io/
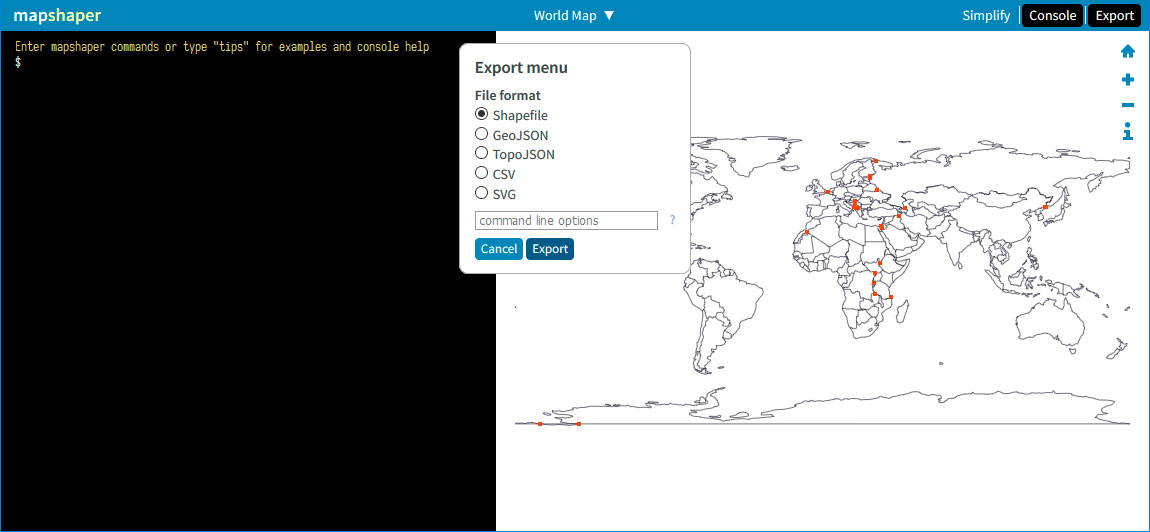
Mapshaper
Keyhole Markup Language (KML)
XML based file format, used to visualize spatial data and modelling information like lines, shapes, 3D images and points in an Google Earth.
Geography Markup Language (GML)
It is used in the Open GIS Consortium for storing geographical data in a standard interchangeable format, It is based on XML.
SVG (Scalable Vector Graphics)
It is an XML-based vector image format for two-dimensional graphics Any program that recognizes XML can display the SVG image.
DWG
DWG is an intern format for AutoCAD. A DWG file is a database of 2D or 3D drawings.
Tidy data

Dataframe
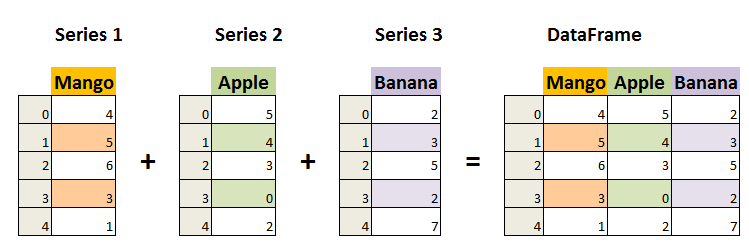
Dataframe
Field-based model
In the field view, the world consists of properties continuously varying across space
Raster
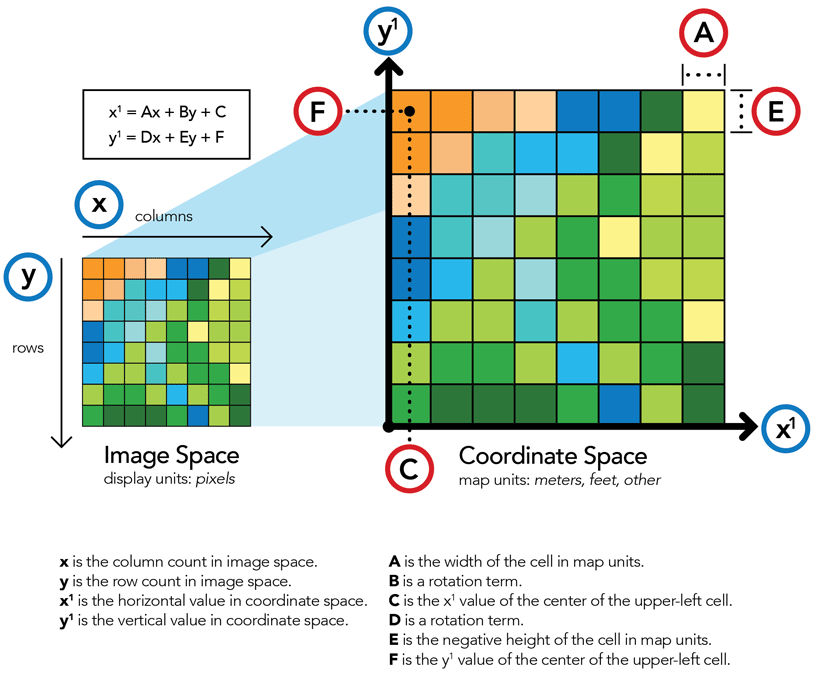
Raster GIS File Format
txt / ASCII (American Standard Code for Information Interchange)
Standard text document that contains plain text. It can be opened and edited in any text-editing or word-processing program
Imagine
Imagine file format by ERDAS. It consists of a single .img file. It is sometimes accompanied by an .xml file which usually stores metadata information about the raster layer.
GeoTiff
A GeoTIFF is a TIF file that ends in a three letter. tif extension just like other TIF files, but a GeoTIFF contains additional tags that provide projection information for that image as specified by the GeoTIFF standard
Raster GIS File Format
Enhanced Compression Wavelet (ECW)
Enhanced Compressed Wavelet (from ERDAS). A compressed wavelet format, often lossy
Network Common Data Form (NetCDF)
netCDF file format with The Climate and Forecast (CF) metadata conventions for earth science data. It allows for direct web-access of subsets/aggregations of maps through OPeNDAP protocol.
HDF5
is an open source file format that supports large, complex, heterogeneous data. HDF5 uses a "file directory" like structure that allows you to organize data within the file in many different structured ways, as you might do with files on your computer
Web mapping
Web mapping
A web map is an interactive display of geographic information, in the form of a web page, that you can use to tell stories and answer questions. Web maps are interactive. The term interactive implies that the viewer can interact with the map. This can mean selecting different map data layers or features to view, zooming into a particular part of the map that you are interested in, inspecting feature properties, editing existing content, or submitting new content, and so on.
Web maps are useful for various purposes, such as data visualization in journalism (and elsewhere), displaying real-time spatial data, powering spatial queries in online catalogs and search tools, providing computational tools, reporting, and collaborative mapping.



Herramientas

Arquitectura

Geoservidor

Web Map Service (WMS)
WMS entrega imágenes de mapas renderizadas (como PNG, JPEG) basadas en datos geográficos. Esto significa que convierte nuestros datos geoespaciales en una imagen de mapa que los usuarios pueden ver, pero con la que no pueden interactuar en términos de manipulación de datos. El uso de WMS es ideal cuando el requisito principal es mostrar una representación visual de los datos geográficos sin necesidad de interactuar con sus elementos individuales.

Web Feature Service (WFS)
WFS ofrece acceso a datos vectoriales geográficos en bruto (como puntos, polilíneas, polígonos). Esto significa que los usuarios pueden interactuar, consultar e incluso modificar directamente tanto los datos espaciales como los atributos. El uso de WFS es ideal para escenarios donde los usuarios necesitan interactuar directamente con los datos geoespaciales y, posiblemente, editarlos.
Web Map Tile Service (WMTS)
Entrega teselas de mapas pre-renderizadas, generalmente en formatos como PNG o JPEG. En lugar de renderizar la vista completa del mapa en tiempo real como lo hace WMS, WMTS utiliza teselas pre-generadas para componer rápidamente una vista de mapa basada en las operaciones de zoom y desplazamiento del usuario. El uso de WMTS es más adecuado para aplicaciones que requieren una navegación y visualización de mapas rápida, donde los datos son relativamente estáticos y no necesitan actualizaciones frecuentes.
Raster tiles: las capas de teselas suelen estar compuestas de imágenes PNG. Tradicionalmente, cada imagen PNG tiene un tamaño de 256 × 256 píxeles.
Vector tiles: las teselas vectoriales se distinguen por la capacidad de rotar el mapa mientras las etiquetas mantienen su orientación horizontal, y por la capacidad de hacer zoom de manera suave—sin la estricta división en niveles de zoom discretos que tienen las capas de teselas ráster.
Tile layers

Tile layers

https://a.tile.openstreetmap.org/2/1/3.png
Zoom level

Zoom level

Vector tiles

Ejemplo
Web Coverage Service (WCS)
WCS proporciona acceso a datos ráster geoespaciales en bruto. A diferencia de WMS, que solo devuelve imágenes de datos, WCS devuelve los datos en bruto que representan los valores reales subyacentes de un conjunto de datos ráster. El uso de WCS es ideal cuando los usuarios necesitan los valores reales de los píxeles de un conjunto de datos ráster. Esto es importante para tareas científicas, analíticas y de modelado donde los datos en bruto, en lugar de la representación visual, son esenciales.

Web Processing Service (WPS)
WPS permite la ejecución de procesos geoespaciales en el lado del servidor. Esto significa que, en lugar de solo recuperar o mostrar datos, los usuarios pueden realizar varias operaciones sobre esos datos, como análisis de buffer, intersección, unión, etc. El uso de WPS es esencial cuando se requieren cálculos geoespaciales en tiempo real, aprovechando las capacidades de procesamiento del lado del servidor.

Data distribution
Measurement scales
Histogramas & bins
Frequency Distribution and Histograms
Frequency distribution table is a table that stores the categories (also called “bins”), the frequency, the relative frequency and the cumulative relative frequency of a single continuous interval variable
The frequency for a particular category or value (also called “observation”) of a variable is the number of times the category or the value appears in the dataset.
Relative frequency is the proportion (%) of the observations that belong to a category. It is used to understand how a sample or population is distributed across bins (calculated as relative frequency = frequency/n )
The cumulative relative frequency of each row is the addition of the relative frequency of this row and above. It tells us what percent of a population (observations) ranges up to this bin. The final row should be 100%.
A probability density histogram is defined so that (i) The area of each box equals the relative frequency (probability) of the corresponding bin, (ii) The total area of the histogram equals 1
Distribución de frecuencia
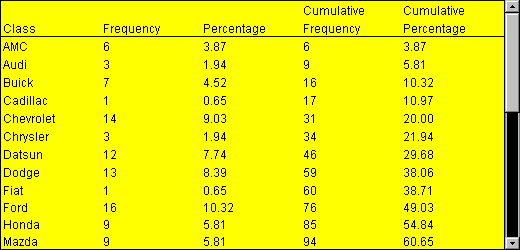
Distribución de frecuencia

Distribución de frecuencia

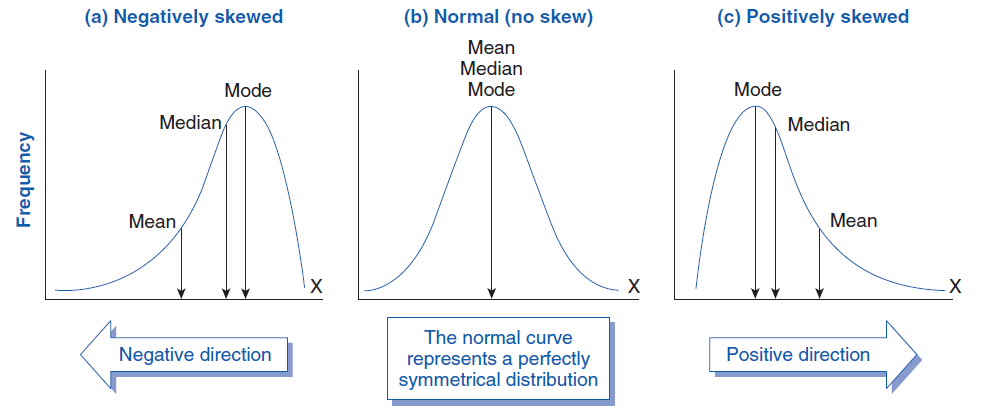
Central Limit Theorem
When we collect sufficiently large samples from a population, the means of the samples will have a normal distribution. Even if the population is not normally distributed.
Box plot
A boxplot is a graphical representation of the key descriptive statistics of a distribution.
The characteristics of a boxplot are
- The box is defined by using the lower quartile Q1 (25%; left vertical edge of the box) and the upper quartile Q3 (75%; right vertical edge of the box). The length of the box equals the interquartile range IQR = Q3 - Q1.
- The median is depicted by using a line inside the box. If the median is not centered, then skewness exists.
- To trace and depict outliers, we have to calculate the whiskers, which are the lines starting from the edges of the box and extending to the last object not considered an outlier.
- Objects lying further away than 1.5 IQR are considered outliers.
- Objects lying more than 3.0 IQR are considered extreme outliers, and those between (1.5 IQR and 3.0 IQR) are considered mild outliers. One may change the 1.5 or 3.0 coefficient to another value according to the study’s needs, but most statistical programs use these values by default.
- Whiskers do not necessarily stretch up to 1.5 IQR but to the last object lying before this distance from the upper or lower quartiles.
Box plot

Box plot

Box plot

QQ plot
The normal QQ plot is a graphical technique that plots data against a theoretical normal distribution that forms a straight line
A normal QQ plot is used to identify if the data are normally distributed
If data points deviate from the straight line and curves appear (especially in the beginning or at the end of the line), the normality assumption is violated.
QQ plot

Scatter plot
A scatter plot displays the values of two variables as a set of point coordinates
A scatter plot is used to identify the relations between two variables and trace potential outliers.
Inspecting a scatter plot allows one to identify linear or other types of associations
If points tend to form a linear pattern, a linear relationship between variables is evident. If data points are scattered, the linear correlation is close to zero, and no association is observed between the two variables. Data points that lie further away on the x or y direction (or both) are potential outliers
Visualización D3js: 4 variables
Statistical Probability Distributions
A statistical distribution describes how values of a variable are spread or dispersed. It tells us the likelihood of different outcomes

Statistical Probability Distributions
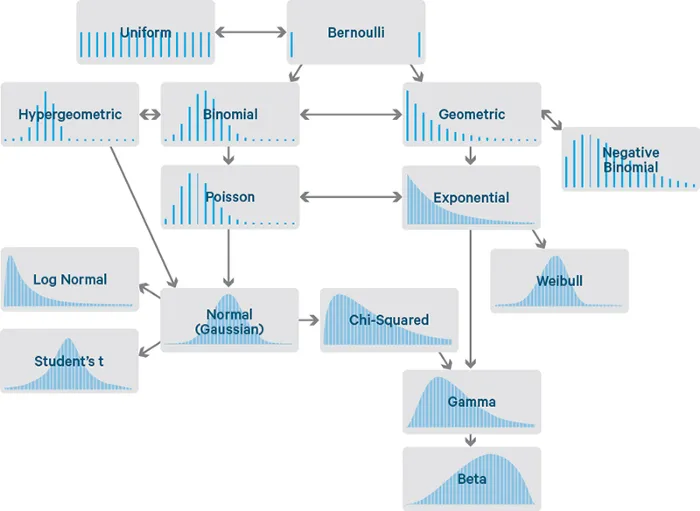
Statistical Probability Distributions

Underlying data distribution

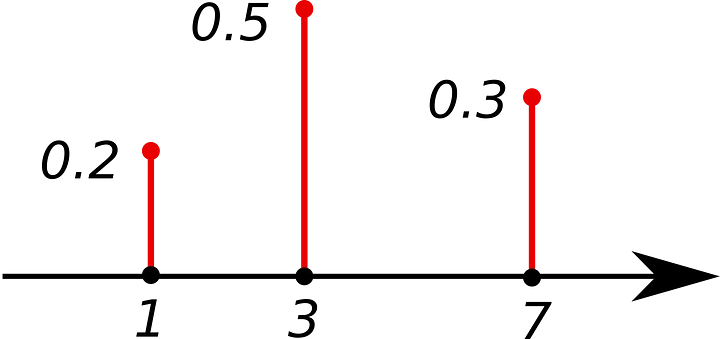
PMF: Probability Mass Function
Returns the probability that a discrete random variable X is equal to a value of x. The sum of all values is equal to 1. PMF can only be used with discrete variables.
PDF: Probability Density Function
It is like the version of PMF for continuous variables. Returns the probability that a continuous random variable X is in a certain range.
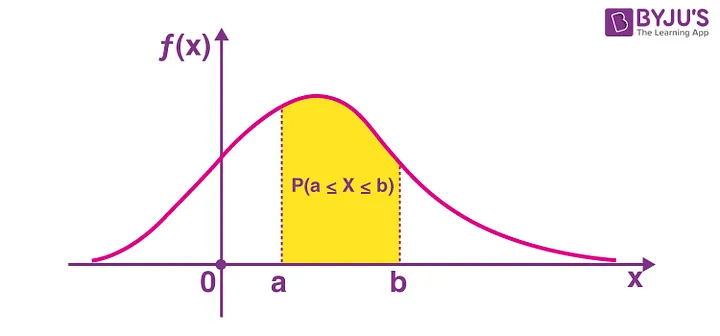
CDF: Cumulative Density Function
Returns the probability that a random variable X takes values less than or equal to x.

Covariance matrix
Covariance is a measure of the extent to which two variables vary together (i.e., change in the same linear direction). Covariance Cov(X, Y) is calculated as:
$cov_{x,y}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1}$where $x_i$ is the score of variable X of the i-th object, $y_i$ is the score of variable Y of the i-th object, $\bar{x}$ is the mean value of variable X, $\bar{y}$ is the mean value of variable Y.
For positive covariance, if variable X increases, then variable Y increases as well. If the covariance is negative, then the variables change in the opposite way (one increases, the other decreases). Zero covariance indicates no correlation between the variables.

Correlation coefficient
Correlation coefficient $r_{(x, y)}$ analyzes how two variables (X, Y) are linearly related. Among the correlation coefficient metrics available, the most widely used is the Pearson’s correlation coefficient (also called Pearson product-moment correlation),
$r_{(x, y)} = \frac{\text{cov}(X,Y)}{s_x s_y}$Correlation is a measure of association and not of causation.
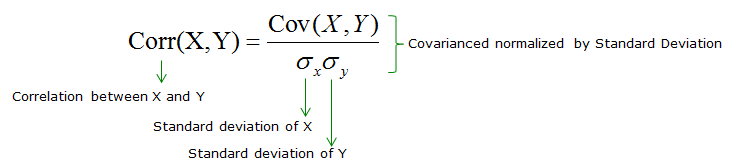

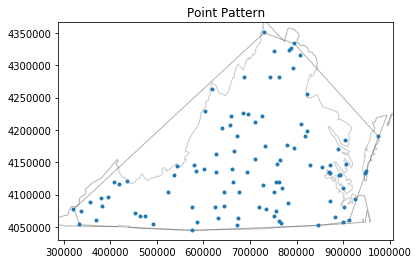
Point Pattern
Point pattern analysis
Análisis de patrones de puntos
Los puntos son entidades espaciales que pueden entenderse de dos maneras fundamentalmente diferentes:
- Los puntos son eventos (análisis sobre DÓNDE ocurren las cosas). Aquí, la ubicación del punto es el dato. No hay otra variable. Solo te interesa saber si hay patrones en esas ubicaciones. Un patrón de puntos consiste en un conjunto de eventos ubicados en ciertos lugares, donde cada evento representa una única instancia del fenómeno de interés.
- Los puntos son lugares donde tomaste una medida (análisis sobre QUÉ VALOR tiene algo en diferentes lugares). Una observación que ocurre en un punto también puede verse como un sitio de medición de un proceso geográficamente continuo subyacente. Este enfoque implica que tanto la ubicación como la medición importan.
Análisis de patrones de puntos
El análisis de patrones de puntos se ocupa de la visualización, descripción, caracterización estadística y modelado de patrones de puntos, tratando de comprender el proceso generador que da lugar y explica los datos observados. Las preguntas comunes en este campo incluyen:
- ¿Cómo se ve el patrón?
- ¿Cuál es la naturaleza de la distribución de los puntos?
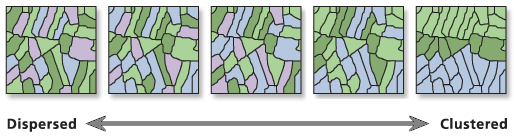
- ¿Existe alguna estructura en la forma en que se disponen las ubicaciones en el espacio? Es decir, ¿los eventos están agrupados o están dispersos?
- ¿Por qué ocurren los eventos en esos lugares y no en otros?
Proceso & Patrón
El proceso se refiere al mecanismo subyacente que está en funcionamiento para generar el resultado que observamos. Debido a su naturaleza abstracta, no lo vemos directamente. Sin embargo, en muchos contextos, el foco principal del análisis es aprender sobre qué determina un fenómeno dado y cómo se combinan esos factores para generarlo. En este contexto, el “proceso” está asociado con el cómo.
Por otro lado, el patrón se refiere al resultado de ese proceso. En algunos casos, es la única evidencia del proceso que podemos observar y, por lo tanto, el único insumo con el que contamos para reconstruirlo. Aunque observable directamente y, quizás, más fácil de abordar, el patrón es solo un reflejo del proceso.
El verdadero desafío no es caracterizar el patrón, sino usarlo para deducir el proceso.
Proceso & Patrón
El Proceso espacial es una descripción de cómo puede generarse un patrón espacial.
Existen tres tipos principales de proceso espacial:
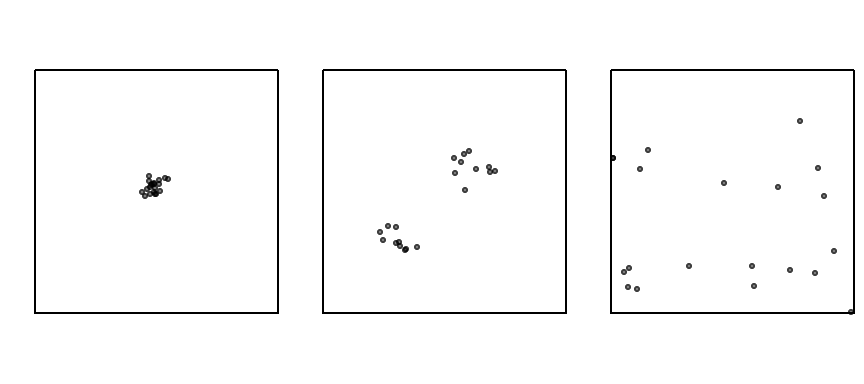
- Aleatorio (CSR – Complete Spatial Randomness): Los eventos se distribuyen sin una estructura reconocible
- Existe una probabilidad igual de ocurrencia de eventos en cualquier ubicación dentro de la región de estudio (también llamado estacionariedad de primer orden).
- La ubicación de un evento es independiente de las ubicaciones de otros eventos (también llamado estacionariedad de segundo orden).
- Disperso (Regular/Uniforme): Es un proceso que hace que los eventos se dispongan lo más alejados posible entre sí; los eventos tienden a distribuirse de manera uniforme.
- Agrupado (Clustered): Los puntos tienden a aparecer juntos en grupos o “clústeres”. Puede ser resultado de un proceso subyacente.
Análisis de patrones de puntos
Existen dos métodos principales (interrelacionados) para analizar patrones de puntos: los métodos basados en la distancia y los métodos basados en la densidad.
- Métodos basados en densidad --> Ubicación absoluta utilizan la intensidad de ocurrencia de eventos en el espacio. Por esta razón, describen mejor los efectos de primer orden. Los métodos de estimación por kernel son ejemplos comunes de este enfoque. En los métodos de conteo por cuadrantes, el espacio se divide en una cuadrícula regular (como una malla de cuadrados o hexágonos) de área unitaria.
- Métodos basados en distancia --> Ubicación relativa emplean las distancias entre eventos y describen los efectos de segundo orden. Estos métodos incluyen el método del vecino más cercano, las funciones de distancia G y F, la función de distancia K de Ripley y su transformación.
Centrograhy

Convex Hull
Quadrant density
This technique requires that the study area be divided into sub-regions (aka quadrats). Then, the point density is computed for each quadrat by dividing the number of points in each quadrat by the quadrat’s area. Quadrats can take on many different shapes such as hexagons and triangles

Kernel Density Function
TEs una técnica no paramétrica que permite estimar la intensidad local de un patrón de puntos en el espacio. En vez de contar cuántos puntos hay en un cuadrado (como en el método de cuadrantes), KDE suaviza la información de los puntos en un mapa continuo.

Kernel Density Function
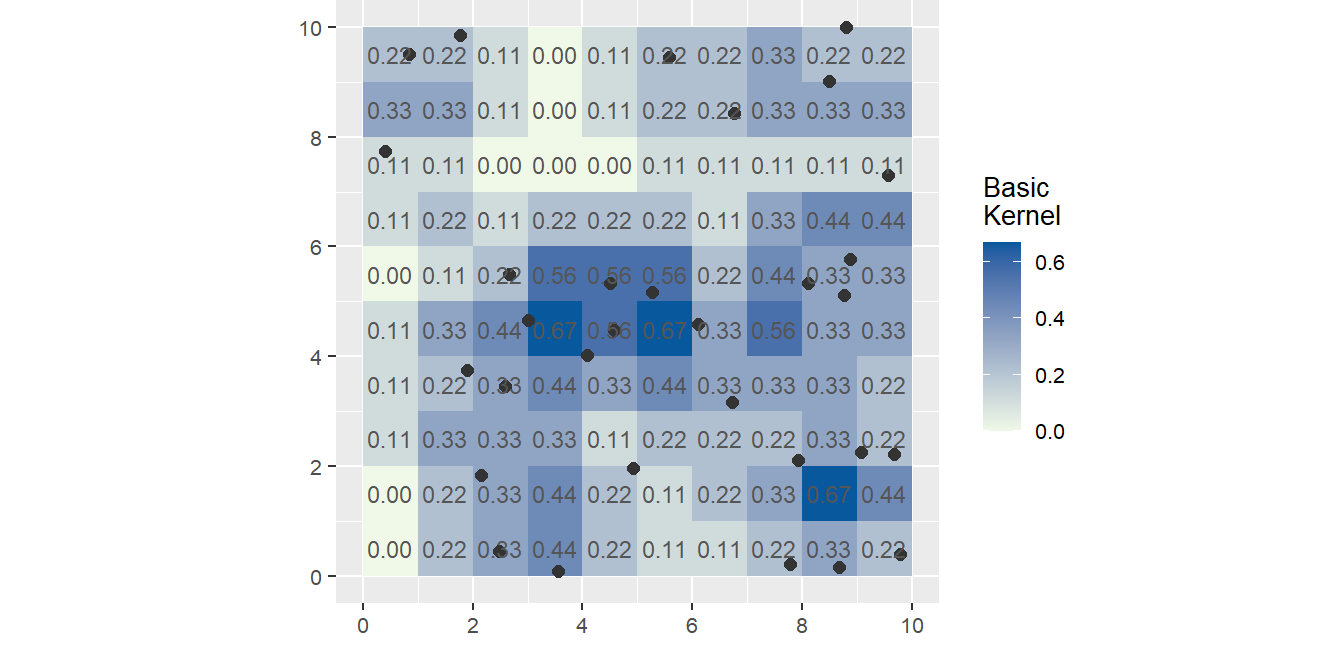
Análisis de vecino más cercano (NN)
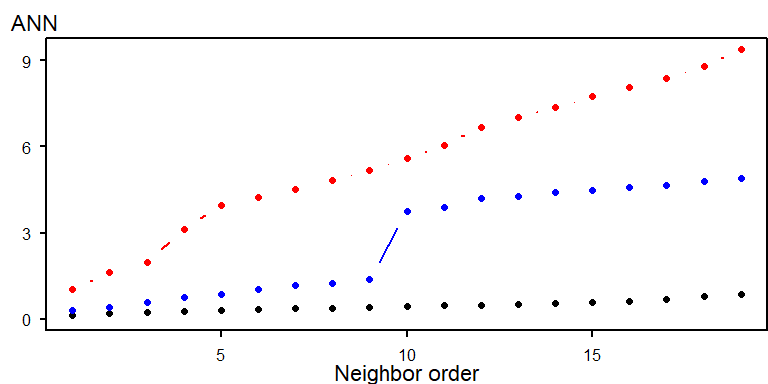
El método compara la distribución espacial observada con una distribución teórica aleatoria. La herramienta de Vecino Más Cercano Promedio (ANN) mide la distancia entre el centroide de cada entidad y el centroide de su vecino más cercano. Luego promedia todas estas distancias al vecino más cercano. Si la distancia promedio es menor que la distancia promedio de una distribución aleatoria hipotética, se considera que la distribución de las entidades analizadas está agrupada. Si la distancia promedio es mayor que la de una distribución aleatoria hipotética, se considera que las entidades están dispersas.

NN analysis

Análisis de vecino más cercano (NN)
Una extensión de esta idea es graficar los valores de ANN para vecinos de diferente orden, es decir, para el punto más cercano, luego el segundo más cercano, y así sucesivamente.
Función K de Ripley
Es un método de análisis espacial para estudiar patrones de puntos basado en una función de distancia. El resultado de la función es el número esperado de eventos dentro de un radio \( d \). Se calcula como una serie de distancias incrementales \( d \) centradas, sucesivamente, en cada uno de los eventos.

Clustering
El objetivo es identificar subgrupos en los datos, de tal forma que los datos en cada subgrupo (clusters) sean muy similares, mientras que los datos en diferentes subgrupos sean muy diferentes.
Distance


- Hierarchical Clustering: descomposición jerárquica utilizando algún criterio, pueden ser aglomerativos (bottom-up) o de separación (top-down). No necesitan K al inicio.
- Partitioning Methods ( (k-means, PAM, CLARA): se construye a partir de particiones, las cuales son evaluadas por algún criterio. Necesitan K al inicio.
- Density-Based Clustering: basados en funciones de conectividad y funciones de densidad.
- Model-based Clustering: se utiliza un modelo para agrupar los modelos.
- Fuzzy Clustering: A partir de lógica difusa se separan o agrupan los clusters.

Clustering

Dendrograma

Dendrograma

Dendrograma


K-means




Método Silhouette

DBScan
DBSCAN is a density-based clustering method, which means that points that are closely packed together are assigned into the same cluster and given the same ID. The DBSCAN algorithm has two parameters, which the user needs to specify:
In short, all groups of at least minPts points, where each point is within ε or less from at least one other point in the group, are considered to be separate clusters and assigned with unique IDs. All other points are considered “noise” and are not assigned with an ID.
DBScan

Modelos Lineales Generalizados (GML)
Modelos Lineales Generalizados (GML)
Los Modelos Lineales Generalizados (GLM) son una extensión de los modelos lineales clásicos (como la regresión lineal) que permiten modelar una variedad más amplia de tipos de datos, incluyendo aquellos que no siguen una distribución normal. Estos modelos son especialmente útiles cuando la variable dependiente sigue una distribución distinta, como una distribución binomial (en el caso de variables de respuesta dicotómicas), una distribución de Poisson (para conteos), o una distribución gamma (para variables continuas positivas).
- Función de enlace (𝑔(⋅)): Establece la relación entre la media de la variable dependiente 𝑌 y los predictores lineales.
- Distribución de la variable dependiente: La variable dependiente 𝑌 sigue una distribución dentro de la familia exponencial (por ejemplo, normal, binomial, Poisson, etc.).
- Predictores lineales: La relación entre los predictores 𝑋1, 𝑋2,…,Xp y la variable dependiente se describe mediante una combinación lineal de los mismos.
\[g(\mathbb{E}[Y_i]) = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots + \beta_p X_{ip}\]
Modelos GLM
Regresión Lineal Gaussiana
\[ \mathbb{E}[Y_i] = \mu_i = \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \]
Regresión Logística
\[ \log\left(\frac{\mu_i}{1-\mu_i}\right) = \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \]
Regresión Poisson
\[ \log(\mu_i) = \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \]
Regresión Binomial Negativa
\[ \log(\mu_i) = \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \]
Regresión Logística
Distribución de la variable dependiente: Binomial \( Y_i \sim \text{Binomial}(n, \mu_i) \)
Función de enlace: Logit (función logística)
Formulación matemática:
\[ \log\left(\frac{\mu_i}{1-\mu_i}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p \]
Este modelo se utiliza cuando la variable dependiente es binaria (por ejemplo, éxito o fracaso).


Odds

Limitaciones de los Odds

Función LOGIT
Sea p(x) la probabilidad de éxito cuando el valor de la variable predictora es x, entonces:
Donde $a$ es el intercepto del modelo, $b$ son los coeficientes del modelo de regresión logística, y $x$ son las variables independientes (predictoras).
$P(y=1) = \frac{1}{1+e^{-(a+\sum bx)}}$Donde, P es la probabilidad de Bernoulli que una unidad de terreno pertenece al grupo de no deslizamientos o al grupo de si deslizamiento. P varía de 0 a 1 en forma de curva “S” (logística).
Odds

Regresión Logística

Regresión Logística

Regresión Logística

Resultado

$R^2$

$R^2$

$R^2$

Regresión con Poisson
Distribución de la variable dependiente: Poisson \( Y_i \sim \text{Poisson}(\mu_i) \)
Función de enlace: Logaritmo natural
Formulación matemática:
\[ \log(\mu_i) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p \]
Este modelo se utiliza cuando la variable dependiente representa un conteo de eventos en un intervalo de tiempo o espacio.
GLM de Poisson
A Poisson distribution is a discrete probability distribution, meaning that it gives the probability of a discrete (i.e., countable) outcome. For Poisson distributions, the discrete outcome is the number of times an event occurs, represented by $k$. You can use a Poisson distribution if:
- Individual events happen at random and independently. That is, the probability of one event doesn’t affect the probability of another event.
- You know the mean number of events occurring within a given interval of time (1D) or space (2D). This number is called $λ$ (lambda), and it is assumed to be constant.
- Two events cannot occur at exactly the same instant or place.
Distribución de Poisson
$$ P(Y_i = y_i) = \frac{\lambda_i^{y_i} e^{-\lambda_i}}{y_i!}, \quad y_i = 0, 1, 2, \ldots $$El modelo lineal generalizado (GML) de Poisson se especifica de la siguiente manera:
$$ \lambda_i = \mathbb{E}[Y_i] = e^{\eta_i}, \eta_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} $$La función de enlace que relaciona la media $\lambda_i$ con la parte lineal $\eta_i$ es:
$$ \eta_i = \log(\lambda_i) $$De esta forma, la media de la distribución de Poisson se relaciona exponencialmente con la combinación lineal de las covariables:
$$ \lambda_i = e^{\beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}} $$Poisson

Poisson

Regresión Binomial Negativa
Distribución de la variable dependiente: Binomial Negativa \( Y_i \sim \text{NegBin}(\mu_i, \theta) \)
Función de enlace: Logaritmo natural
Formulación matemática:
\[ \log(\mu_i) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p \]
Este modelo se utiliza cuando la variable dependiente es un conteo de eventos, pero hay sobredispersión (la varianza es mayor que la media), lo que no se captura adecuadamente con el modelo de Poisson.
Tipos de ceros en datos de conteo
Cuando modelamos eventos como deslizamientos, los ceros en los datos pueden surgir de al menos tres fuentes:
Ceros estructurales (verdaderos ceros)
Ejemplo: Lugares donde realmente no pueden ocurrir deslizamientos (e.g., lagos, llanuras totalmente estables).
Ceros aleatorios (cero por casualidad)
Ejemplo: Zonas propensas a deslizamientos donde podrían haber ocurrido, pero no ocurrieron durante el periodo observado.
Ceros por omisión o errores de observación
Ejemplo: Eventos que sí ocurrieron, pero no se registraron por limitaciones en los inventarios (e.g., imágenes satelitales de baja resolución) o falta de monitoreo.
Modelos Zero-Inflated
Los modelos de conteo clásicos como Poisson o binomial negativa suponen que los ceros ocurren como parte del proceso natural. Pero en muchos contextos reales (como deslizamientos), hay más ceros de los que esos modelos predicen.
- Una parte binaria (modelo logístico) que predice la probabilidad de estar en el grupo "siempre cero".
- Una parte de conteo (binomial negativa) que modela el número de eventos si no está en el grupo "siempre cero".
Areal data
Discrete
Geovisualización
Choropleth maps
Choropleth maps are thematic maps in which areas are rendered according to the values of the variable displayed
Cloropleth maps are used to obtain a graphical perspective of the spatial distribution of the values of a specific variable across the study area.
There are two main categories of variables displayed in choropleth maps:
- Spatially extensive variables: each polygon is rendered based on a measured value that holds for the entire polygon. Ej. total population
- Spatially intensive variables: the values of the variable are adjusted for the area or some other variable. Ej. population density
Choropleth maps
Breaks
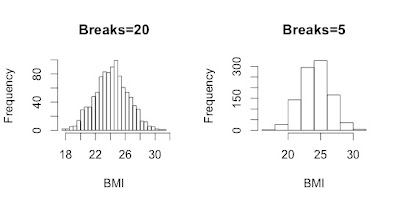
Breaks

Breaks

Spatial association
Spatial dependence
Formal property that measures the degree to which near and distant things are related
Refers to systematic spatial changes that are observed as clusters of similar values or a systematic spatial pattern.
Spatial heterogeneity
Spatial heterogeneity refers to structural relationships that change with the location of the object. These changes can be abrupt (e.g. countryside–town) or continuous.
Spatial heterogeneity refers to the uneven distribution of a trait, event, or relationship across a region
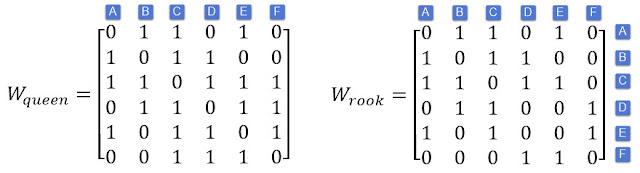
Spatial weight matrix (W)
Spatial weights are numbers that reflect some sort of distance, time or cost between a target spatial object and every other object in the dataset or specified neighborhood. Spatial weights quantify the spatial or spatiotemporal relationships among the spatial features of a neighborhood.

Neighborhood
Neighborhood in the spatial analysis context is a geographically localized area to which local spatial analysis and statistics are applied based on the hypothesis that objects within the neighborhood are likely to interact more than those outside it.
- Neighbours by contiguity: areas that share common boundaries
- neighbours by distance: areas will be defined as neighbours if they are within a specified radius
Spatial Relationships
Adjacency (Contiguity)
Adjacency can be thought of as the nominal, or binary, equivalent of distance. Two spatial entities are either adjacent or they are not.
Contiguity among features means the features have common borders. We have three types of contiguity:
- Rook Contiguity: the features share common edges
- Bishop Contiguity: the features share common vertices (corners)
- Queen Contiguity: the feature share common edges and corners.
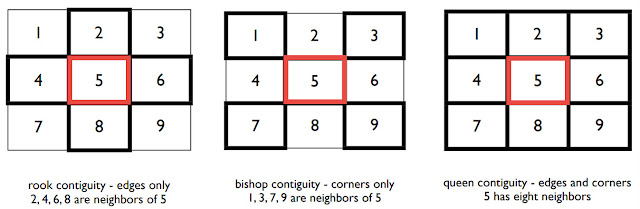
Contiguity



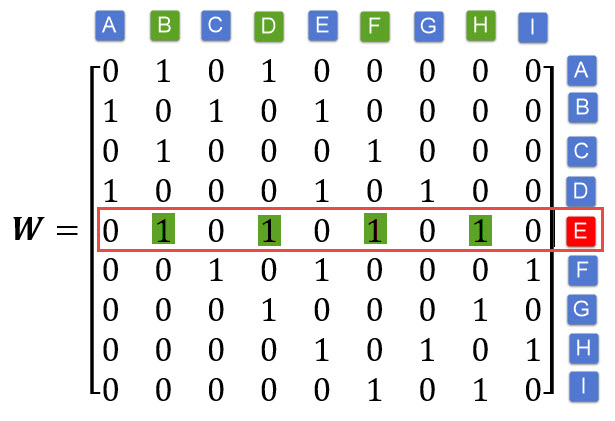
Ej.

Matrix of k nearest neighbours (knn)

Standarized Spatial Weights
Row standardization is recommended when there is a potential bias in the distribution of spatial objects and their attribute values due to poorly designed sampling procedures.
Row standardization should also be used when polygon features refer to administrative boundaries or any type of man-made zones.
Ej.

Spatial lag
Spatial lagis when the dependent variable y in place i is affected by the independent variables in both place i and j.




Global indicator of Spatial Association (GISA)
The measures (test statistics) related to the existence of spatial autocorrelation in data, that is, focusing on whether there is any spatial autocorrelation in the data
Indice de Moran
The positive value of global Moran implies the existence of a positive autocorrelation, and conversely, the negative value implies the existence of a negative autocorrelation

If there is no relationship between Income and Income_lag, the slope will be close to flat (resulting in a Moran’s I value near 0).



Moran’s I at different lags
Moran’s I at different spatial lags defined by a 50 km width annulus at 50 km distance increments. Red dots indicate Moran I values for which a P-value was 0.05 or less.
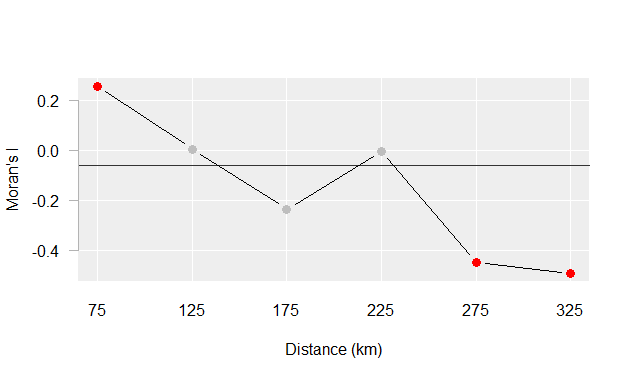
Moran’s I at different lags

Moran’s I at different lags

Moran’s I at different lags

Local indicators of Spatial Association (LISA)
A local statistic is any descriptive statistic associated with a spatial data set whose value varies from place to place.

Moran´s I scatter plot

Moran´s I scatter plot
Red points and polygons highlight counties with high income values surrounded by high income counties. Blue points and polygons highlight counties with low income values surrounded by low income counties.
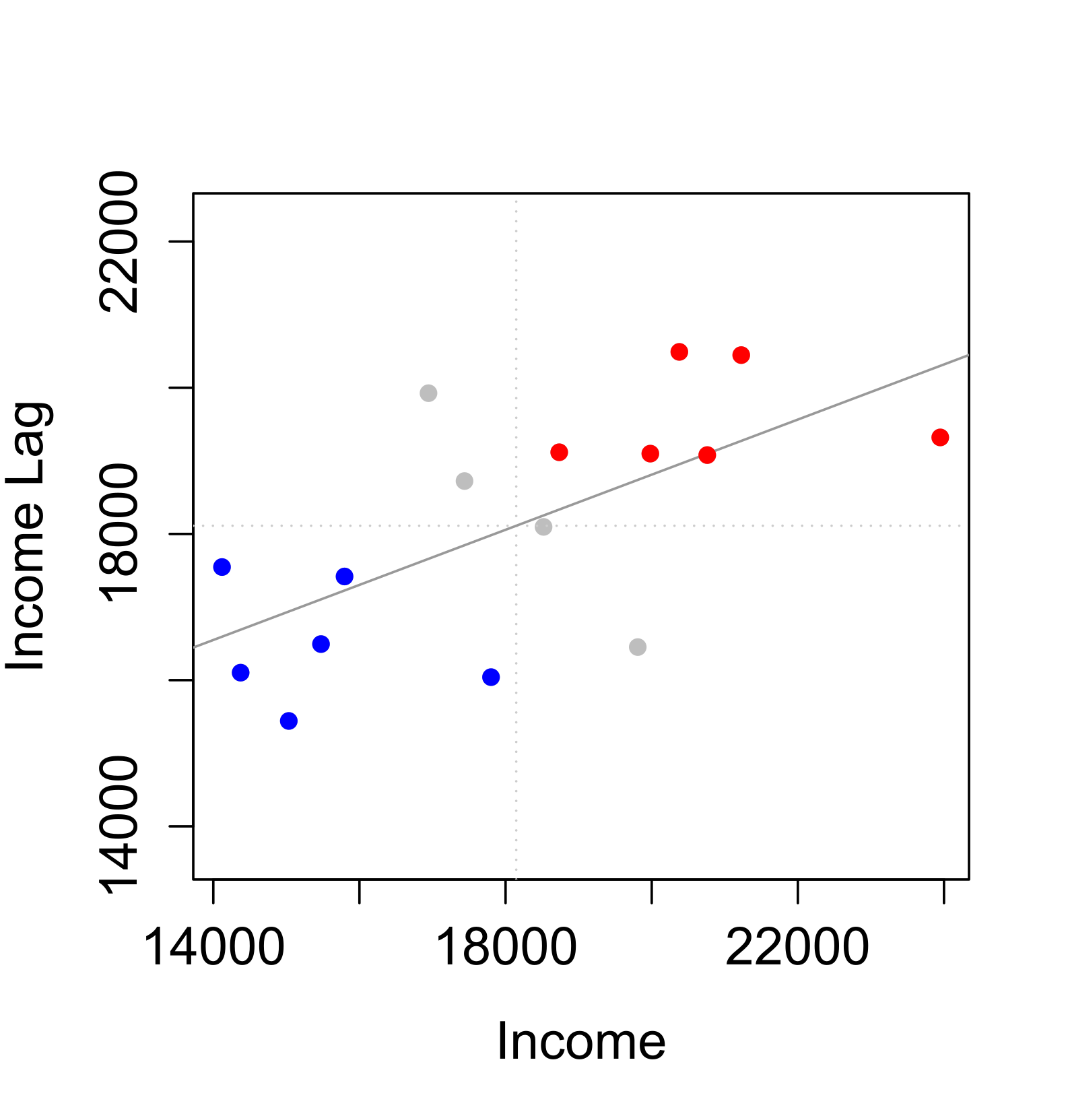
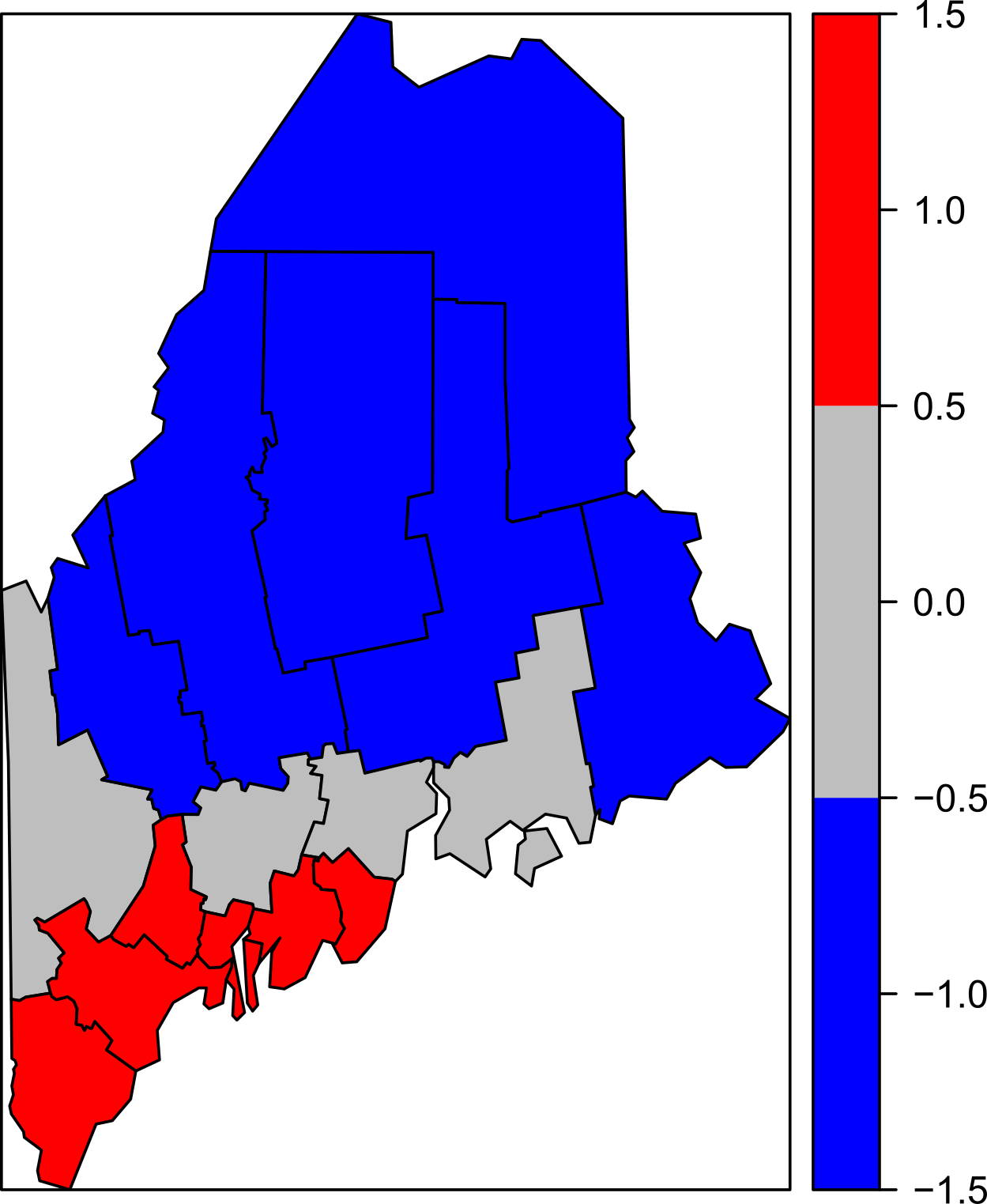
Moran´s I scatter plot

Moran´s I scatter plot

Moran´s I scatter plot

Spatial cluster

Spatial Regression Models
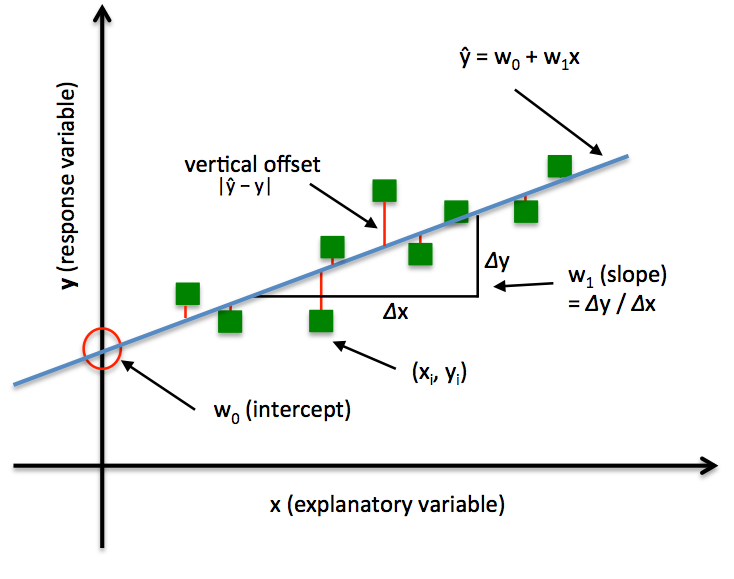
Simple Linear Regression model
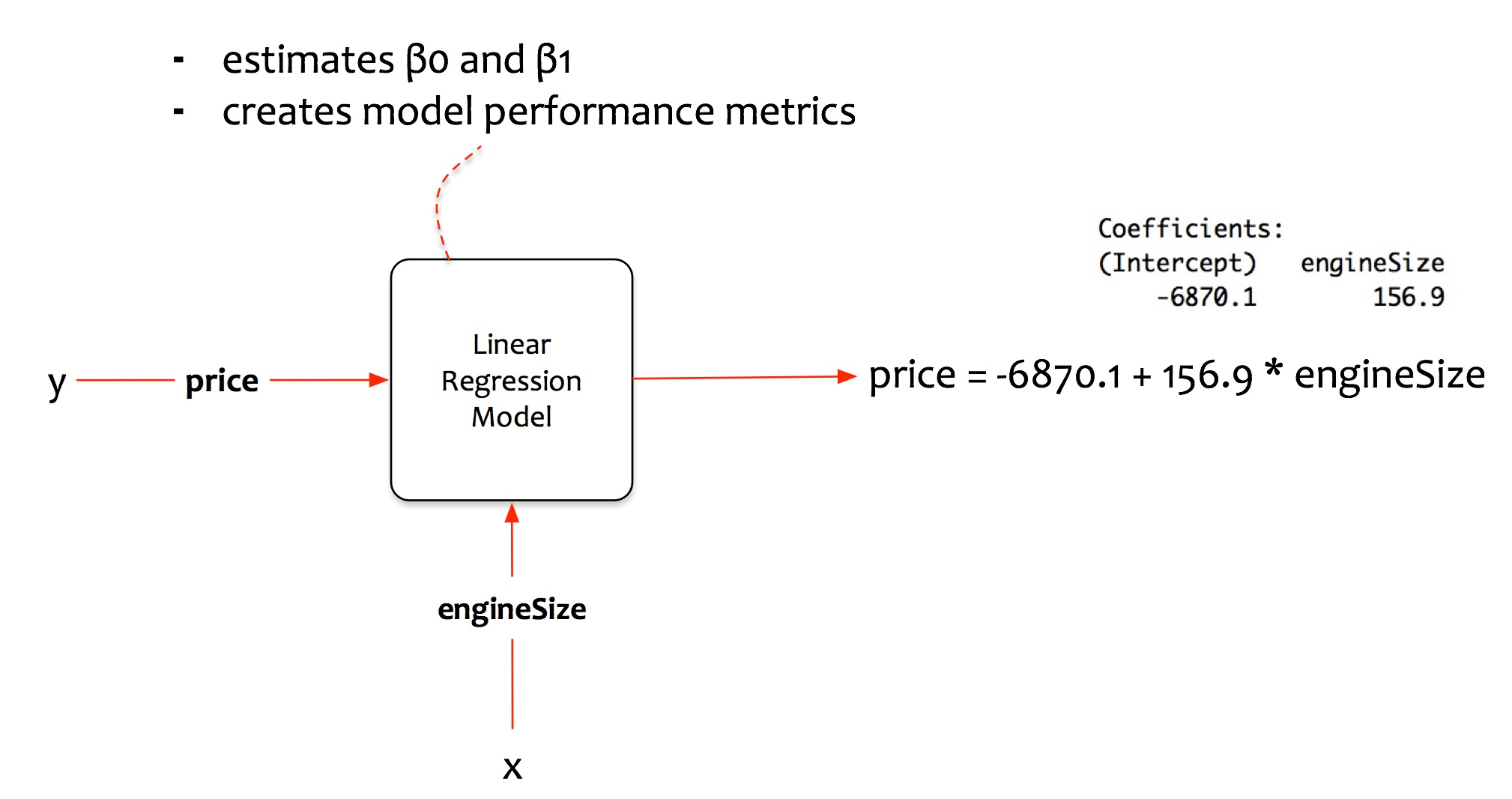
Regresión lineal
Multivariate regression model
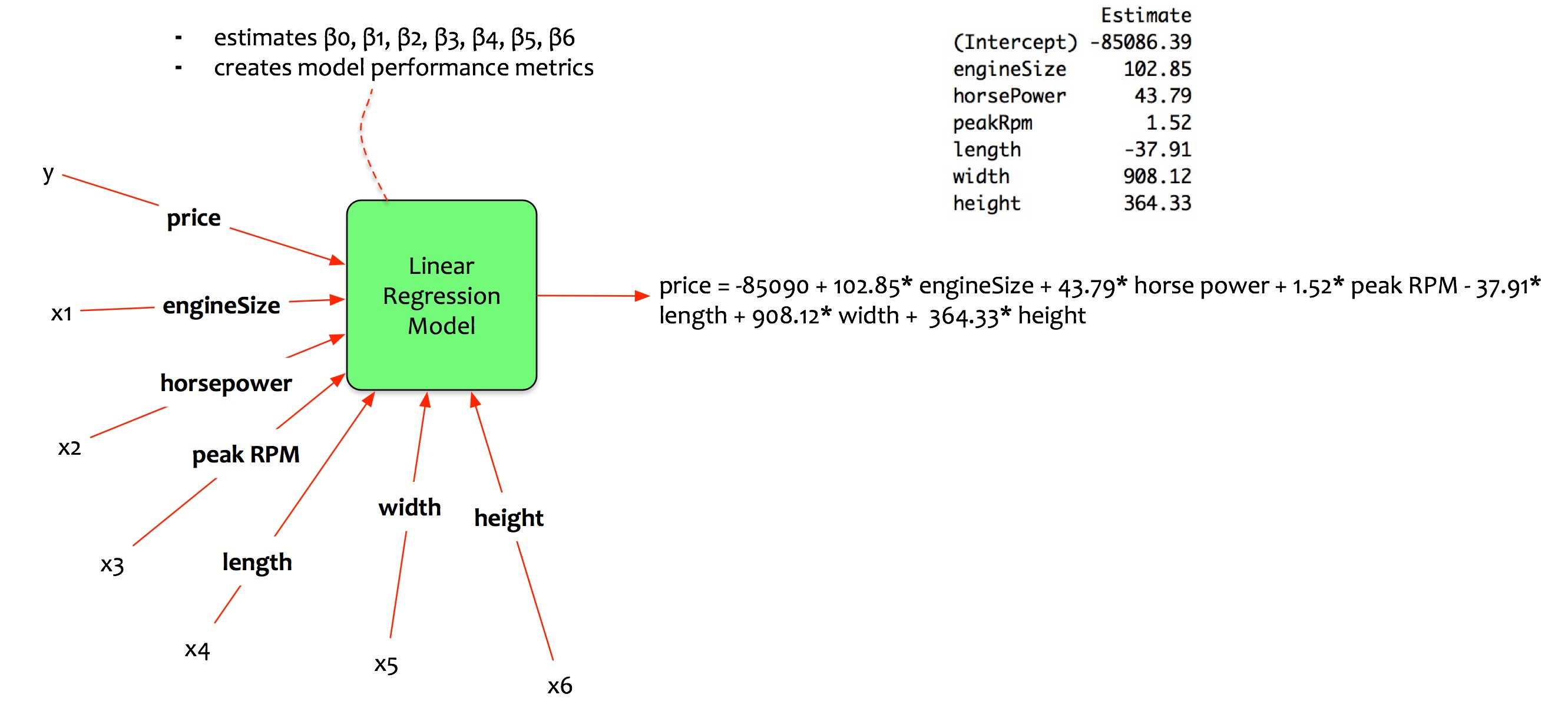
Multivariate regression model

Ordinary least squares regression (OLS)
Assumptions
- Linear relationship between the dependent and independent variables
- Multivariate normality: the residual of the linear model should be normally distributed
- No multicolinearity between independent variables, i.e. they should not correlate between each other
- Homoscedasticity: the errors/residuals should have constant variance (no trends)
- No autocorrelation: residuals (errors) in the model shoul not be correlqated in any way
Resultados

$R^2$

Adjusted $R^2$

Spatial regression

Spatial regression

Modelos de regresión para Heterogeneidad Espacial
Regimenes Espaciales
Simson`s paradox

Simson`s paradox

Simson`s paradox

Heterogeneidad espacial

Heterogeneidad espacial

Heterogeneidad espacial

Modelos multiniveles (jerárquicos)

No jerarquico

Random intercepto (fixed effect)

Random slope (regimes)

Random slope & intercepto

Modelo multinivel - fixed effect

Modelo multinivel - regimenes

Modelo multinivel

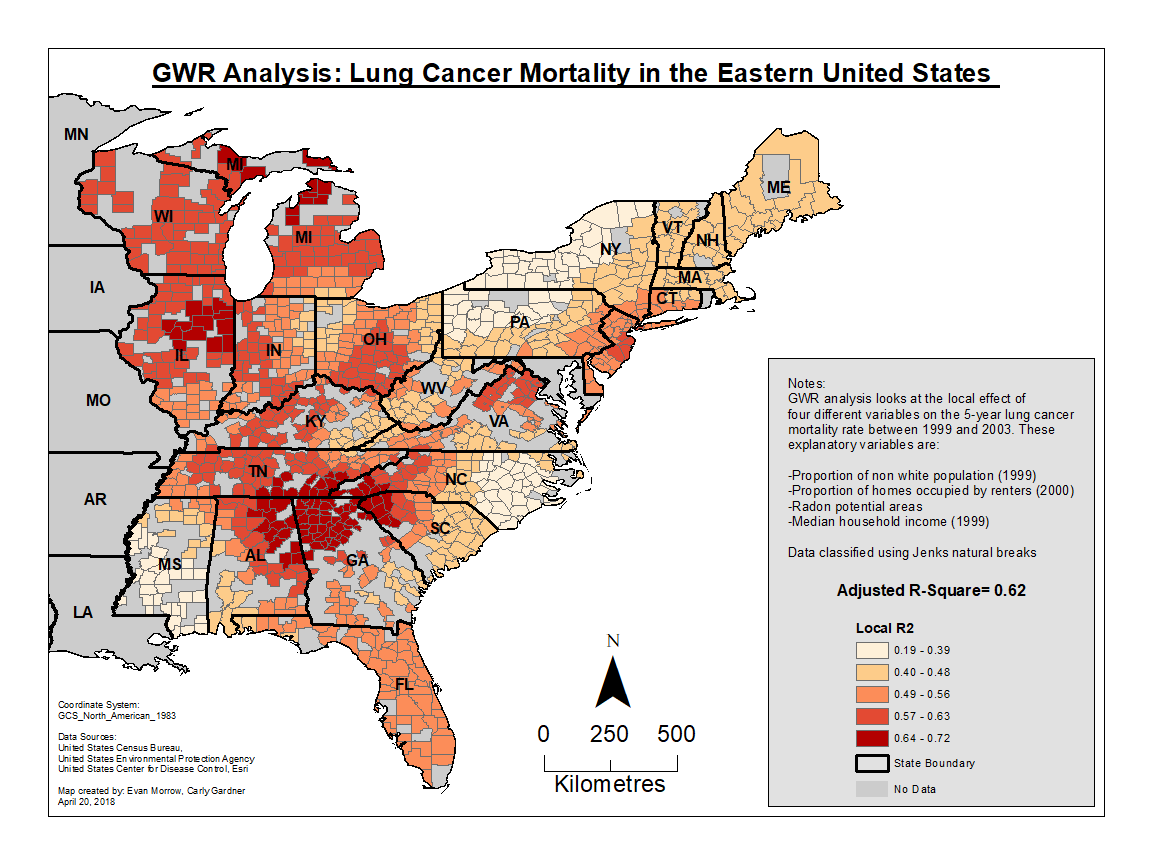
Geographycally Weighted Regresion (GWR)
Geographycally Weighted Regresion (GWR)
where $(ui, vi)$ are the spatial coordinates of the observations $i$, and $β_k (ui, vi)$ are the coefficients estimated at those locations.
Thus, in contrast to global LRMs, GWR conducts local regression at a series of locations to estimate local coefficients (the geographical part of GWR), using observations weighted by their distances to the location at the center of the moving window/kernel (the weighted part).
Parameters
Bandwidth is the distance band or number of neighbors used for each local regression equation and is perhaps the most important parameter to consider for Geographically Weighted Regression, as it controls the degree of smoothing in the model.
It can be based on either Number of Neighbors or Distance Band. When Number of Neighbors is used, the neighborhood size is a function of a specified number of neighbors, which allows neighborhoods to be smaller where features are dense and larger where features are sparse. When Distance Band is used, the neighborhood size remains constant for each feature in the study area, resulting in more features per neighborhood where features are dense and fewer per neighborhood where they are sparse.
Parameters
The power of GWR is that it applies a geographical weighting to the features used in each of the local regression equations. Features that are farther away from the regression point are given less weight and thus have less influence on the regression results for the target feature; features that are closer have more weight in the regression equation. The weights are determined using a kernel, which is a distance decay function that determines how quickly weights decrease as distances increase. The Geographically Weighted Regression tool provides two kernel options in the Local Weighting Scheme parameter, Gaussian and Bisquare.
Single bandwidth
a single bandwidth is used in GWR under the assumption that the response-to-predictor relationships operate over the same scales for all of the variables contained in the model. This may be unrealistic because some relationships can operate at larger scales and others at smaller ones. A standard GWR will nullify these differences and find a “best-on-average” scale of relationship non-stationarity (geographical variation)
Geographycally Weighted Regresion (GWR)

Geographycally Weighted Regresion (GWR)

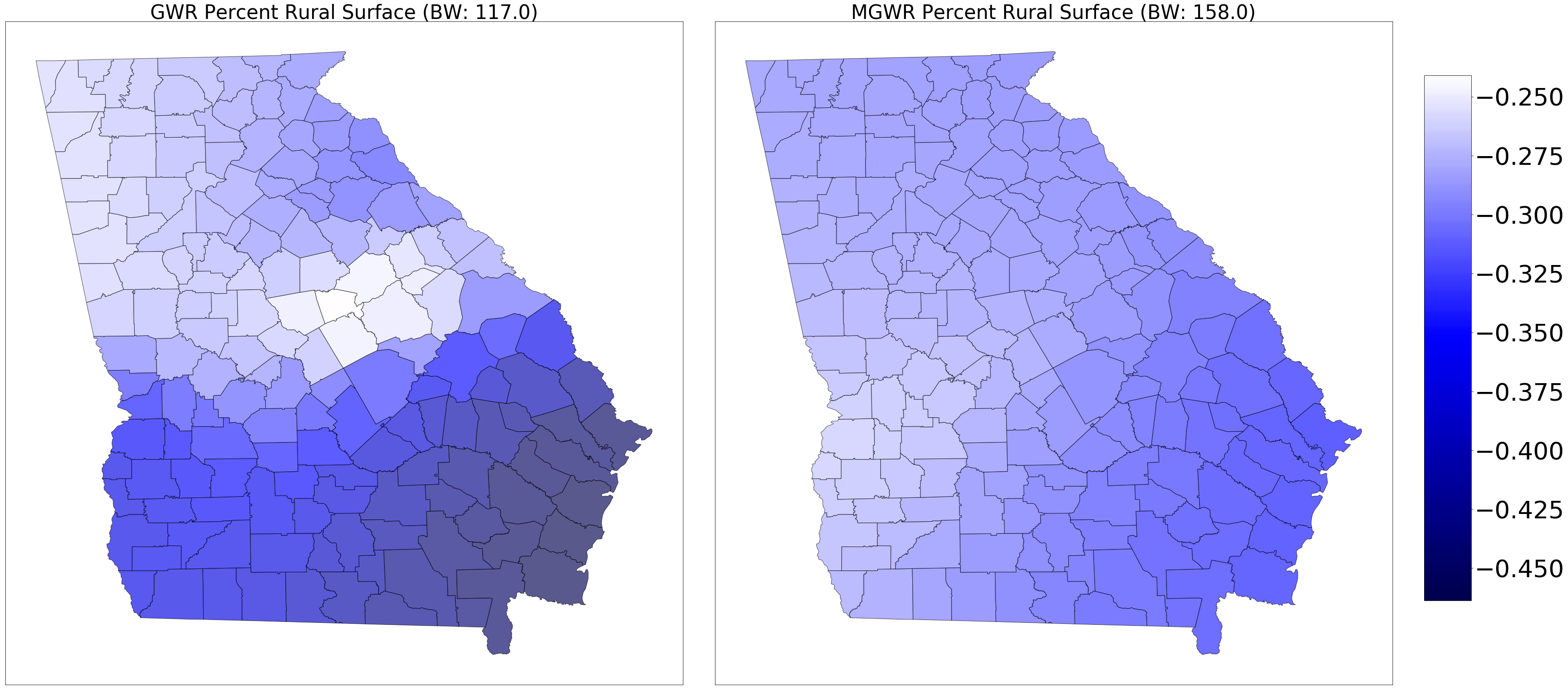
Adaptativo

Fijo (distancia)

Distribución del error
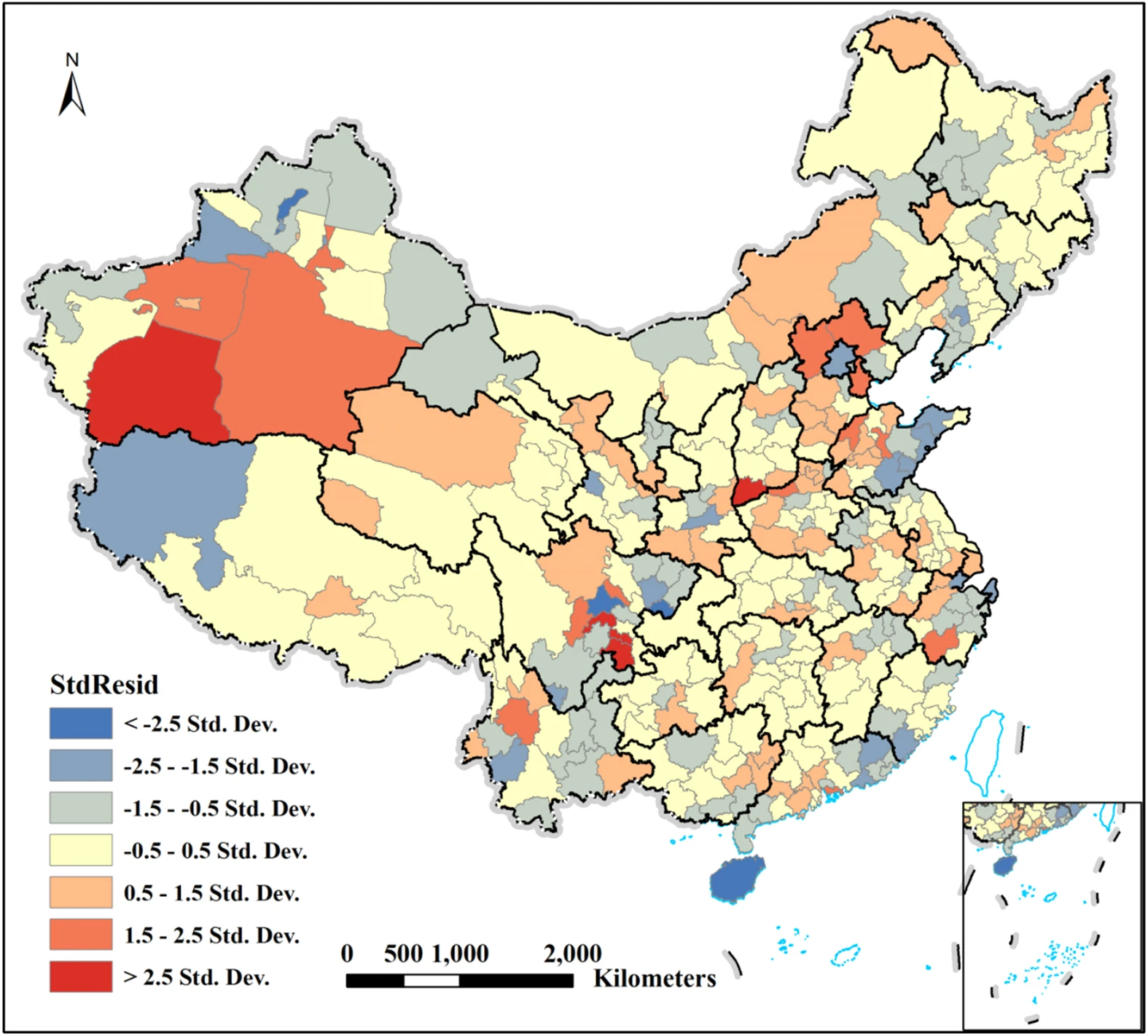
Modelos de regresión para Dependencia Espacial
Modelos autoregresivos SAR
SAR
SAR models account for spatial dependence by including a spatial lag of the dependent variable, error term or exogenous variables. Essentially, they add an autoregressive component that takes into account the weighted average of neighboring values. SAR models are typically specified in the form:
$y = \rho Wy + X\beta + \epsilon$
Joint Distribution in SAR
The SAR model’s joint distribution of the spatial effects y is derived directly from this equation:
$y=(I−ρW)^{−1}(Xβ+ϵ)$
SAR uses a single, global equation involving W to directly specify the joint distribution across all locations.
Dense covariance matrix ($\sum$)
$\sum=(I-\rho W)^{-1}(I-\rho W)^{-T}$


SAR
SAR is formulated as a global process, where the spatial relationships affect the entire dataset simultaneously. The SAR model requires matrix inversion, which can be computationally challenging for large datasets.
SAR Models interpret the spatial effects by including a lag term of the dependent variable, capturing how the value at one location is influenced by the values of all its neighbors. This kind of specification is more aligned with the concept of spatial spillover, meaning that the outcome in one region directly influences the outcomes in neighboring regions.
Modelos autoregresivos

Modelos autoregresivos

Modelos autoregresivos CAR
CAR
CAR models are based on a conditional specification of the dependent variable. Unlike SAR, the CAR model is defined using the conditional distribution of a particular value, given the values of its neighbors. CAR models are generally written in the form:
$y_i=X_iβ+y_i∣y_{-i}+ϵ_i$
$y_i∣y_{-i} ∼N(∑_jϕ_{ij}y_j,τ^2)$
CAR
CAR is formulated using local conditional distributions. This approach leads to a specification where the model conditions on neighboring units, making CAR easier to interpret in a local spatial context. The precision matrix (inverse of the covariance matrix) in a CAR model has a sparse structure, which often makes CAR models more computationally efficient, especially for large spatial datasets.
Precision matrix
$Q=D-W$
Donde D es el número de vecinos


Bayes's theorem

Teorema de Bayes





Conditional probability
A conditional probability is a probability that measures the probability of one event given another event. Intuitively, it is just a proportion of event A’s probability under the occurrence of event B’s.

Joint probability
A joint probability is a probability that calculates probabilities (or likelihoods) of two events that co-occur.

Marginal probability
A marginal probability is a probability of a single event occurring. When a single event occurs with other events, we can decompose it by joint probability with each event.

Joint Distribution in CAR
In the CAR model, although we don’t specify the joint distribution directly, we can derive it from the set of conditional distributions using properties of Markov Random Fields.
The resulting joint distribution for $u$ in a CAR model is represented by a precision matrix (inverse of the covariance matrix), which is sparse. This sparse structure means that only neighboring locations have direct dependencies, unlike SAR’s dense structure.
Mathematically, the joint distribution of $u$ in a CAR model can be expressed as:
$P(u) \propto \exp \left( -\frac{1}{2} u^T Q u \right)$
Intrinsic CAR models (ICAR)
In ICAR models, the precision matrix Q is often singular (non-invertible), which means that the joint distribution does not have a unique covariance matrix. This results in non-identifiability of the random effects in an absolute sense.
To make the model identifiable, ICAR models typically impose a constraint on the spatial random effects, such as a sum-to-zero constraint (e.g., $\sum u_i = 0$). This allows for relative spatial effects, where the values are interpreted relative to the mean of the spatial region rather than as absolute values.
Locally Dependent Structure: In ICAR, the random effect at each location depends only on the neighboring locations, not on any fixed “global” effect. This is why ICAR models are often preferred for applications that require purely local dependencies.
Leroux CAR
Flexible Precision Matrix: The Leroux CAR model has a precision matrix that can be adjusted to avoid singularity, making it possible to estimate a proper covariance structure.
Mixing Parameter: A parameter $\lambda$ (often called the spatial dependence parameter) controls the strength of spatial dependence: (i) If $\lambda = 1$, the model behaves like an ICAR model, with strong spatial dependence. (ii) If $\lambda = 0$, the model assumes independence across locations. (iii) For values between 0 and 1, the model interpolates between independence and spatial dependence, allowing for partial spatial smoothing.
Proper Priors: By adjusting $\lambda$, the Leroux CAR can provide a proper (non-singular) prior distribution, which can help in avoiding identifiability issues and allows the covariance structure to be better specified.
Besag-York-Mollié (BYM) Model
This model combines ICAR for spatial effects and unstructured random effects, allowing for both spatially structured and unstructured variability.
Interpretación de la dependencia espacial
La dependencia espacial puede interpretarse de dos formas:
- Omitir variables (latent): dependencia debida a factores no observados.
- Interacción con vecinos (spillover): resultado del proceso de interacción espacial.
| Modelo | Tipo de dependencia | ¿Spillover observable? | ¿Estructura latente? |
|---|---|---|---|
| SAR (Spatial Autoregressive) |
Global (interacción en WY) | Sí | No |
| SDM (Spatial Durbin Model) |
Global + local (WY y WX) | Sí | No |
| CAR (Conditional Autoregressive) |
Local condicional (Yi | Yj) | No | Sí |
Interpretación clave del modelo CAR
- No implica causalidad ni retroalimentación espacial.
- Captura autocorrelación en los efectos aleatorios espaciales.
Field model
Continuos
Geostatistics
Geostatistics
The type of spatial statistical analysis dealing with continuous field variables is named “geostatistics”
Geostatistics focus on the description of the spatial variation in a set of observed values and on their prediction at unsampled locations
Spatial interpolation
techniques used with points that represent samples of a continuous field are interpolation methods
Here, our point data represents sampled observations of an entity that can be measured anywhere within our study area
There are many interpolation tools available, but these tools can usually be grouped into two categories: deterministic and interpolation methods
Proximity interpolation
It was introduced by Alfred H. Thiessen more than a century ago. The goal is simple: Assign to all unsampled locations the value of the closest sampled location. This generates a tessellated surface whereby lines that split the midpoint between each sampled location are connected thus enclosing an area. Each area ends up enclosing a sample point whose value it inherits.
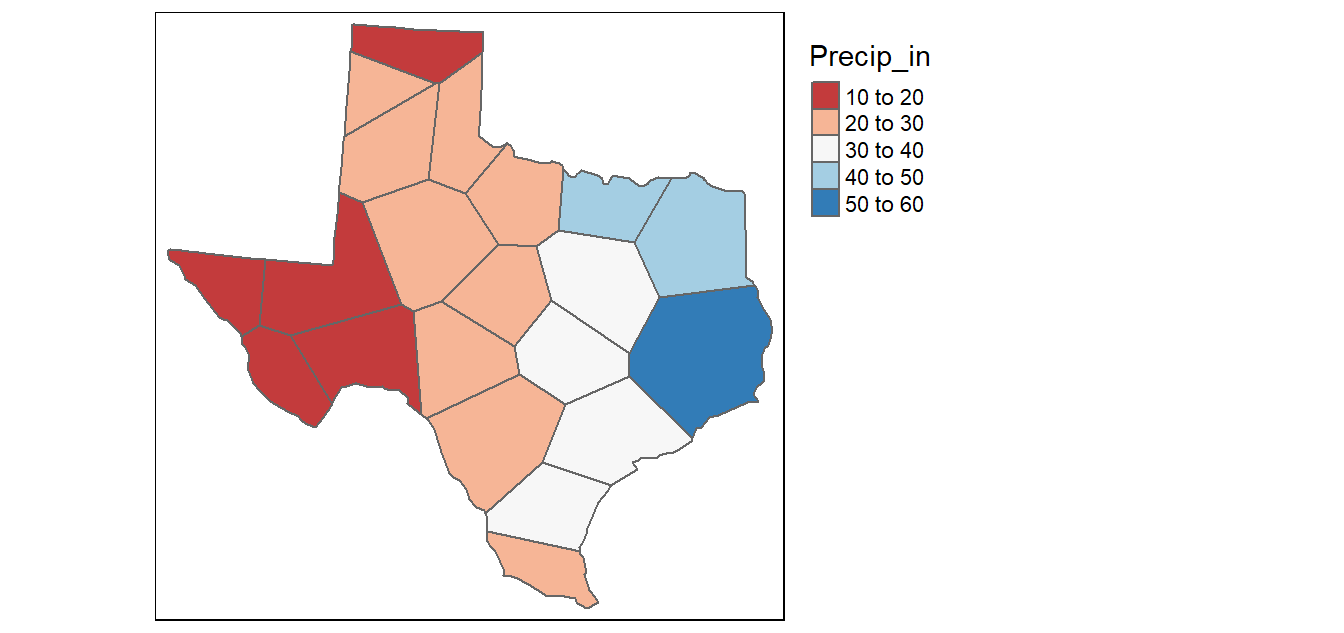
Voronoi diagram

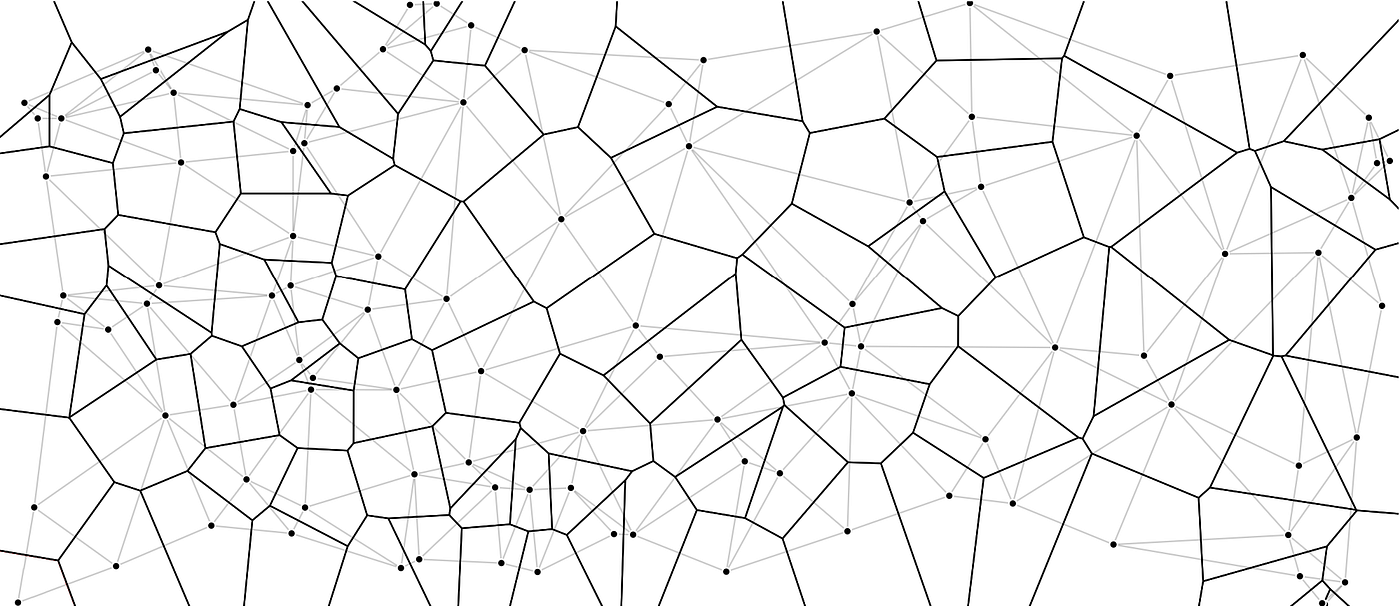
Voronoi & Delanauy triangulation
Inverse Distance Weighted (IDW)
The IDW technique computes an average value for unsampled locations using values from nearby weighted locations. The weights are proportional to the proximity of the sampled points to the unsampled location and can be specified by the IDW power coefficient.
$\hat{Z_j} = \frac{\sum_i{Z_i / d ^ n_{ij}}}{\sum_i{1 / d ^ n_{ij}}}$So a large n results in nearby points wielding a much greater influence on the unsampled location than a point further away resulting in an interpolated output looking like a Thiessen interpolation. On the other hand, a very small value of n will give all points within the search radius equal weight such that all unsampled locations will represent nothing more than the mean values of all sampled points within the search radius.
Kriging
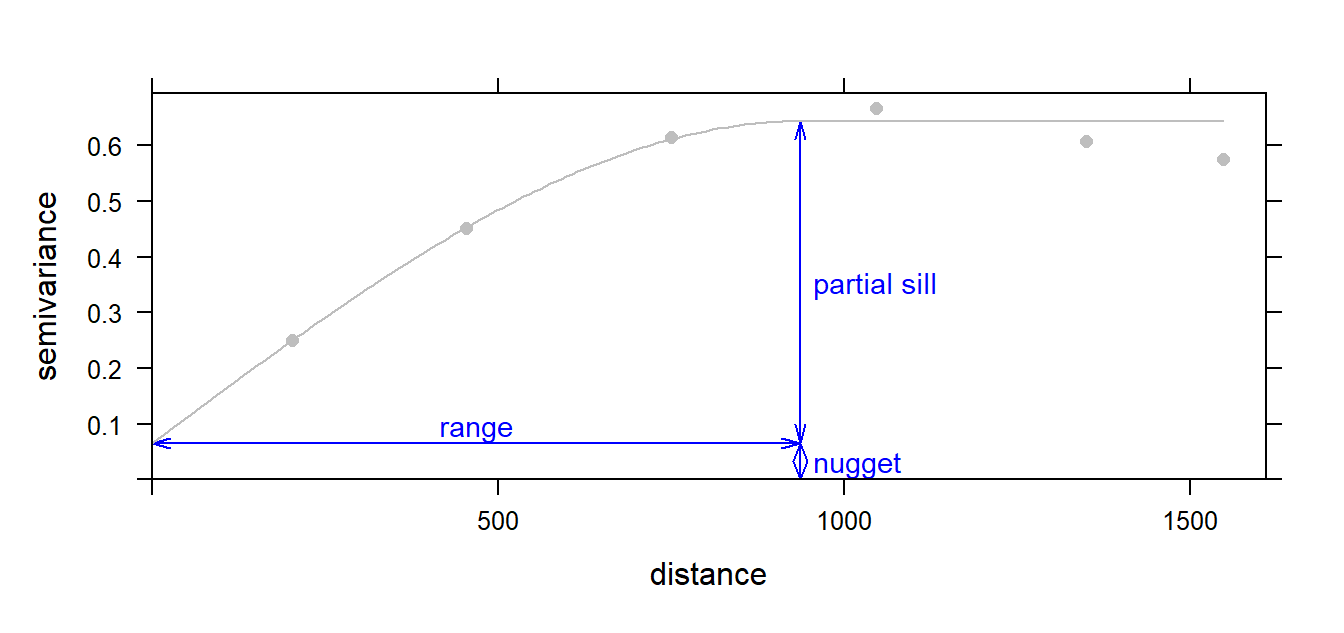
Several forms of kriging interpolators exist: ordinary, universal and simple just to name a few. This section will focus on ordinary kriging (OK) interpolation. This form of kriging usually involves four steps:
- Removing any spatial trend in the data
- Computing the experimental variogram, $γ$ , which is a measure of spatial autocorrelation.
- Defining an experimental variogram model that best characterizes the spatial autocorrelation in the data.
- Interpolating the surface using the experimental variogram.
- Adding the kriged interpolated surface to the trend interpolated surface to produce the final output.
We are interested in how these attribute values vary as the distance between location point pairs increases. We can compute the difference, $γ$, in values by squaring their differences then dividing by 2.
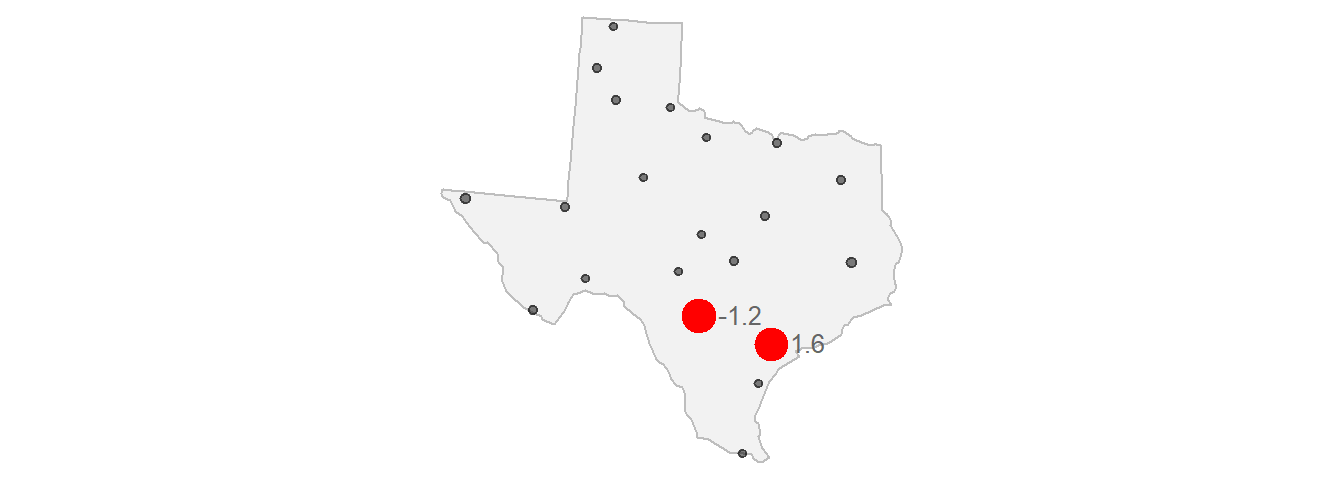 $\gamma = \frac{(Z_2 - Z_1) ^ 2}{2} = \frac{(-1.2 - (1.6)) ^ 2}{2} = 3.92$
$\gamma = \frac{(Z_2 - Z_1) ^ 2}{2} = \frac{(-1.2 - (1.6)) ^ 2}{2} = 3.92$
Experimental variogram
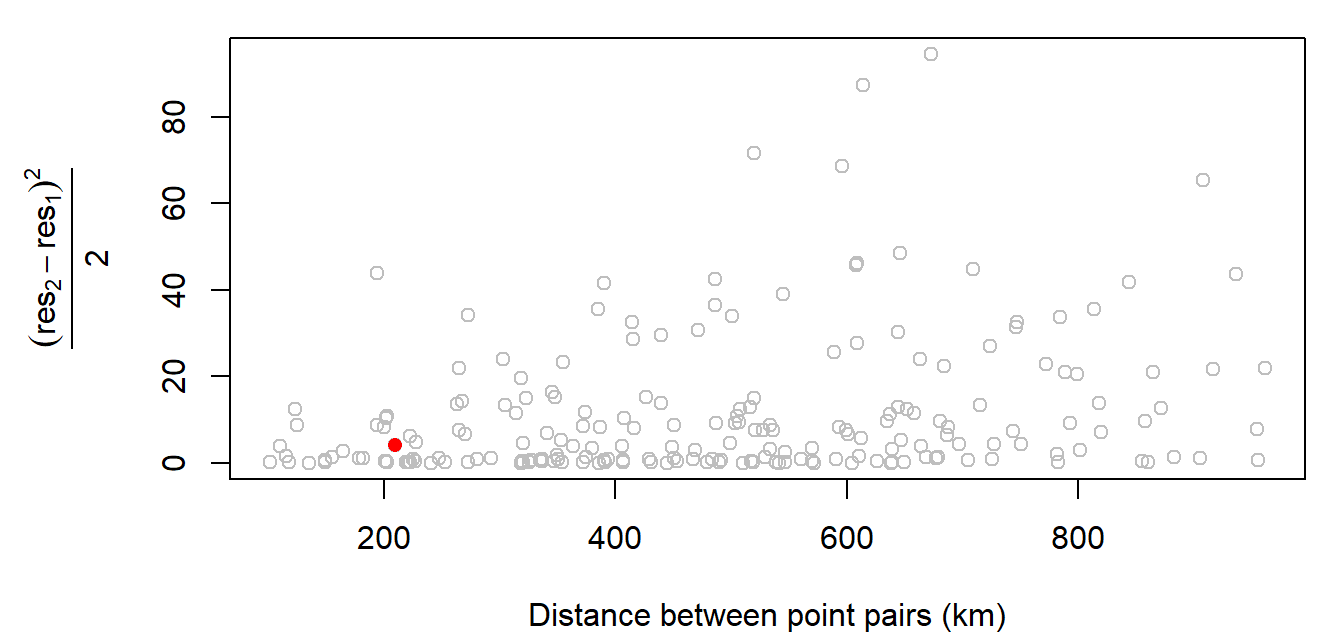
Experimental variogram
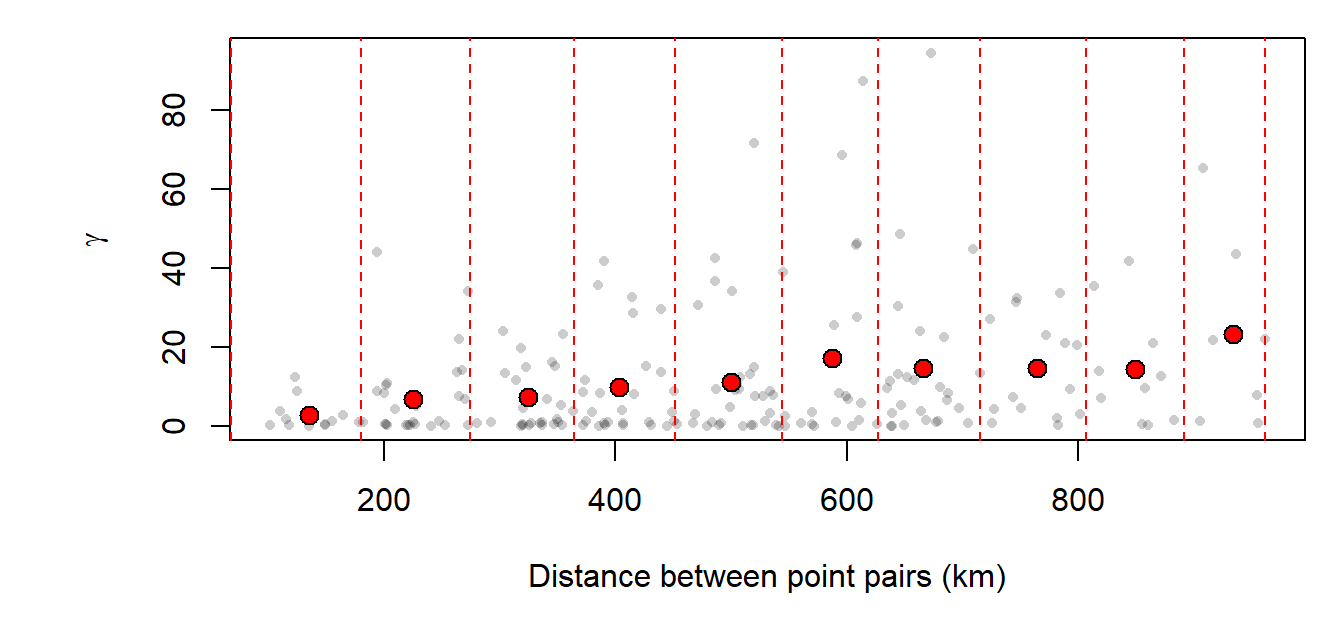
Experimental semivariogram

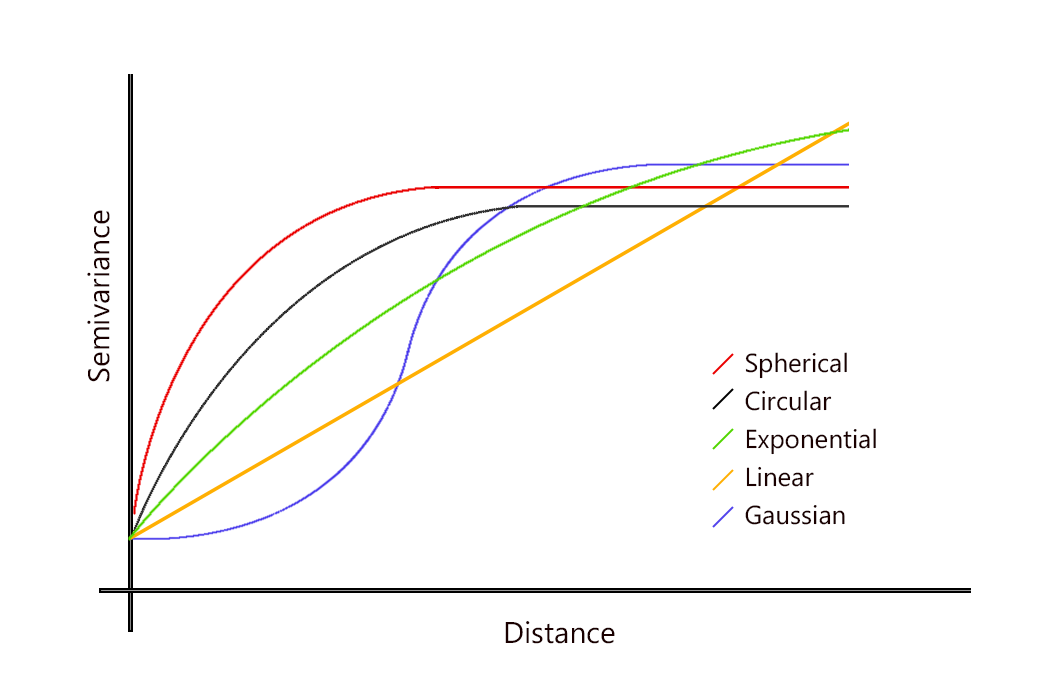
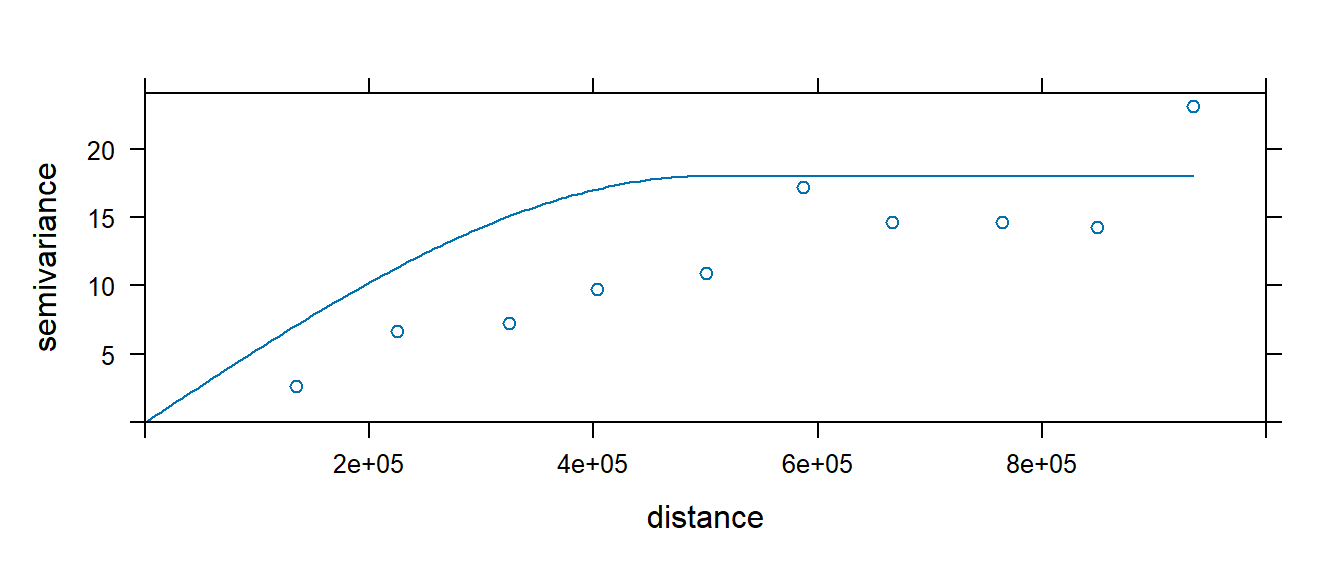
Variogram models
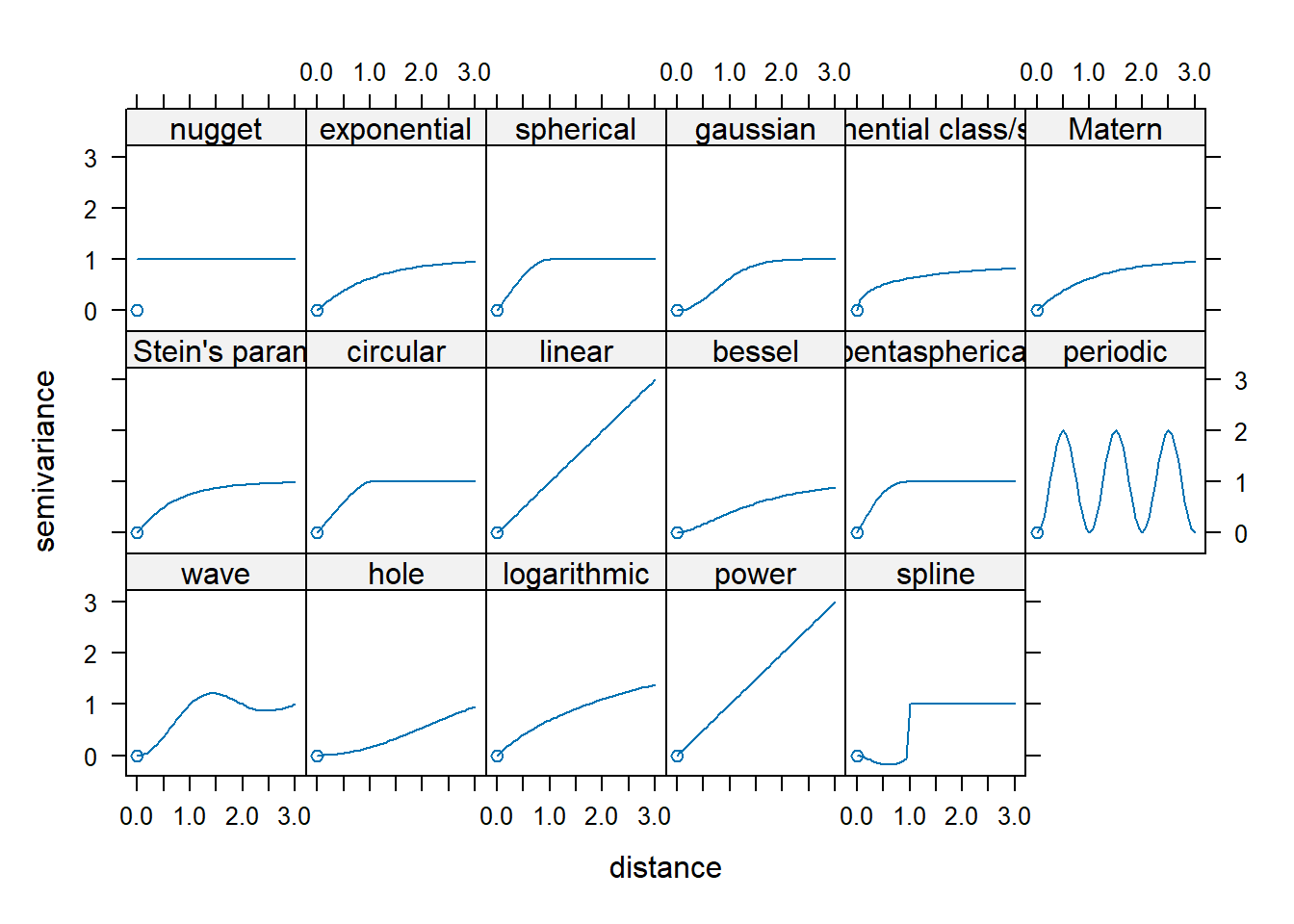
Variogram models
Parameters in a variogram model
Spherical model fit
Gaussian Processes
Spatial Gaussian process (SGP)
A spatial Gaussian process (SGP) refers to a stochastic process frequently employed to model data exhibiting spatial, temporal, or spatiotemporal dependence. A common approach to modeling process $Y(s)$ is by utilizing a spatial linear mixed effects model:
$Y(s)=\mu(s)+w(s)+\epsilon(s)$
the residual component can be decomposed into two parts: a spatial component ($w(s)$) and a unstructured component ($\epsilon(s)$) $iid$. The spatial component can be modeled as a stationary spatial Gaussian process with zero mean and a covariance function $w(s)~SGP(0,\sum)$.
Distribución Gaussiana multivariada
Multivariate Gaussian distribution is the joint probability of Gaussian distribution with more than two dimensions. It has the probability density function below.


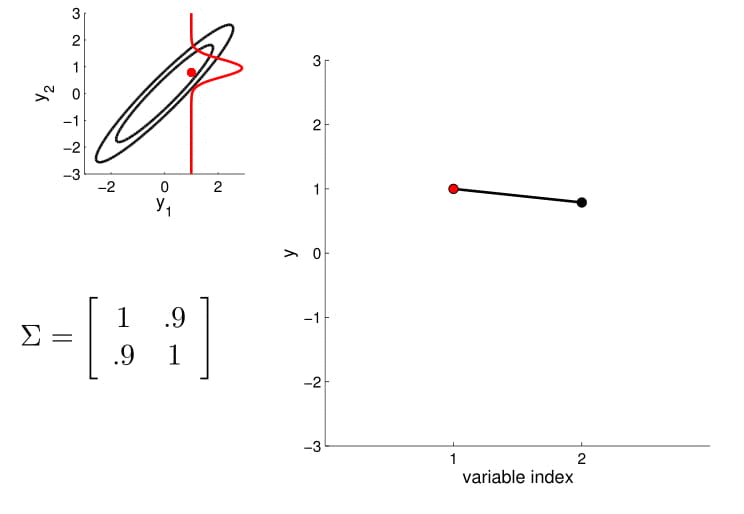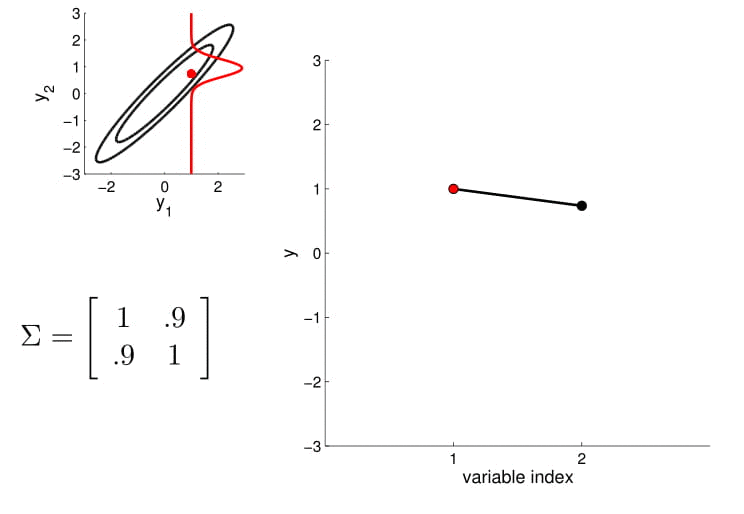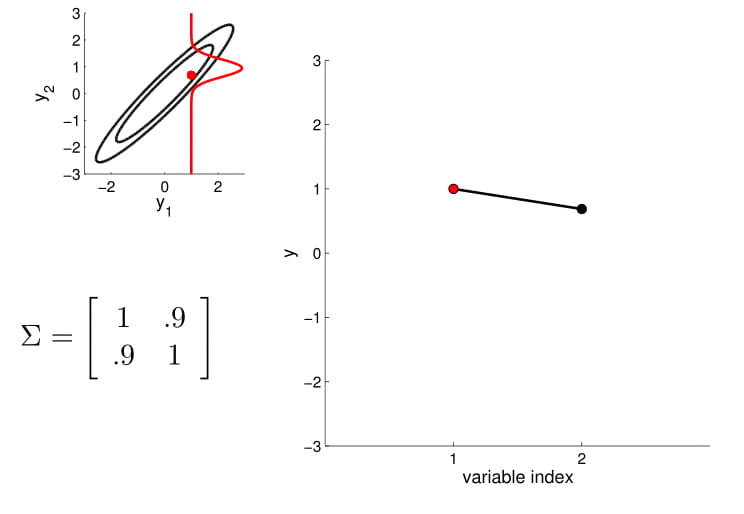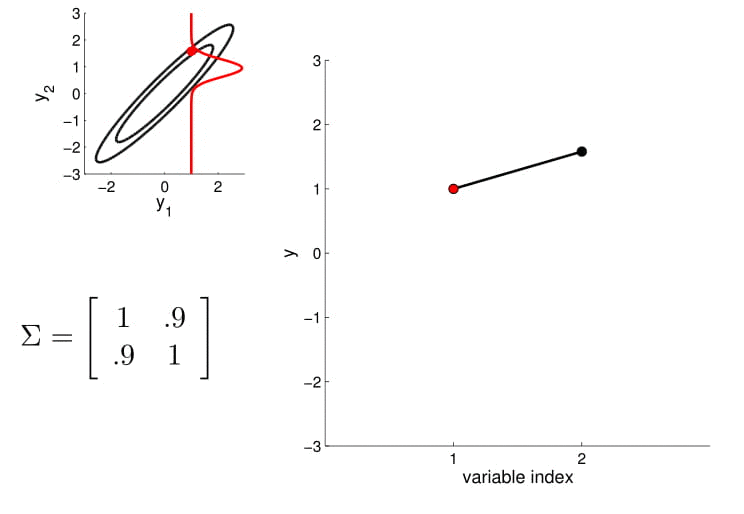
Distribución marginal


Distribución condicionada

Matriz de covarianza
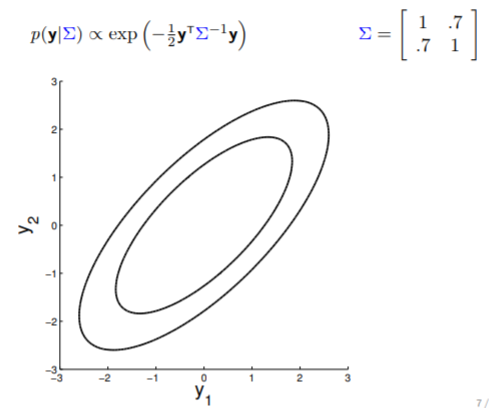
Matriz de covarianza

Matriz de covarianza

2D Gaussian

2D Gaussian
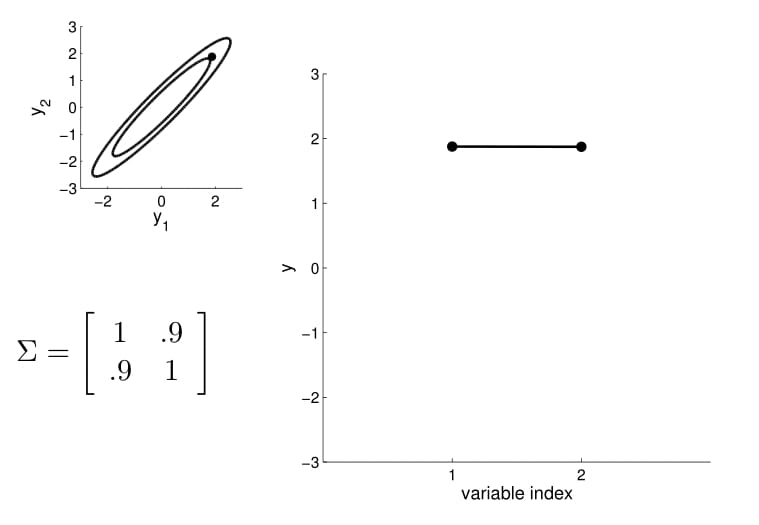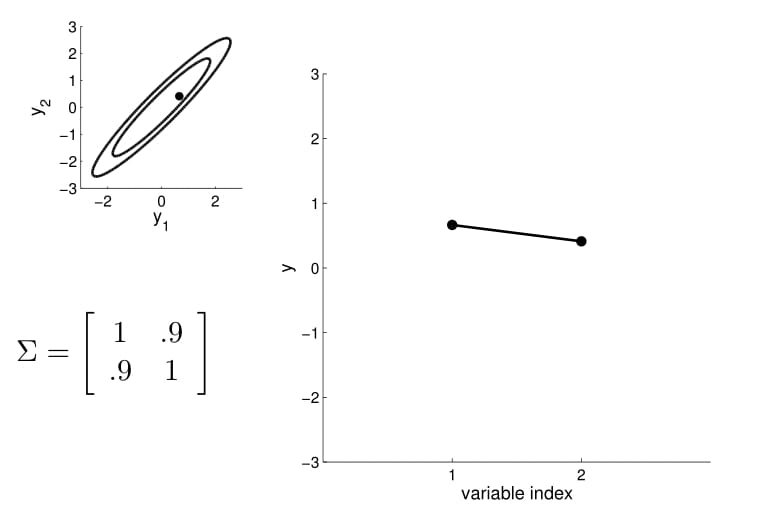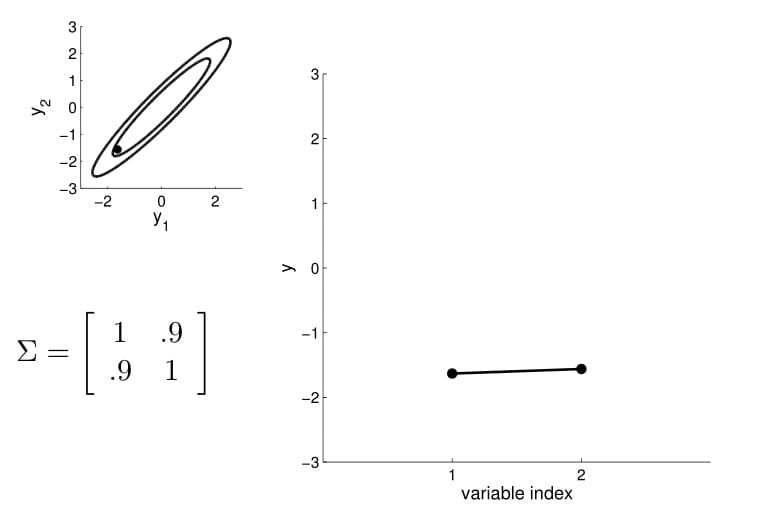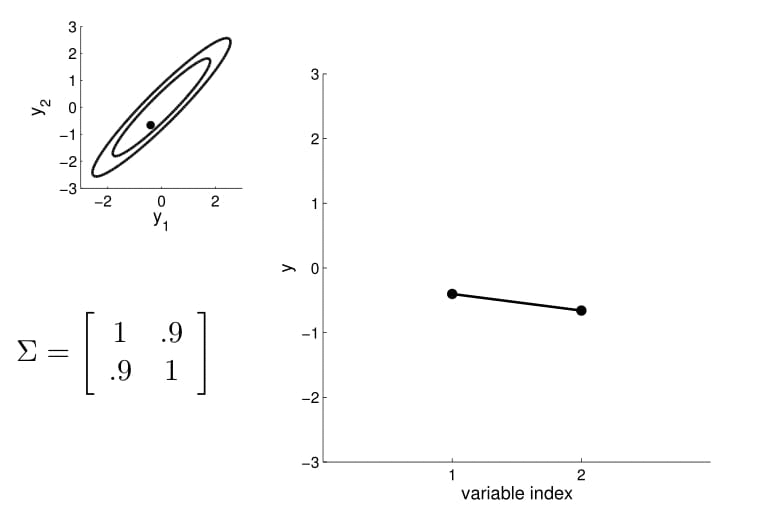
2D Gaussian
5D Gaussian

5D Gaussian

20D Gaussian
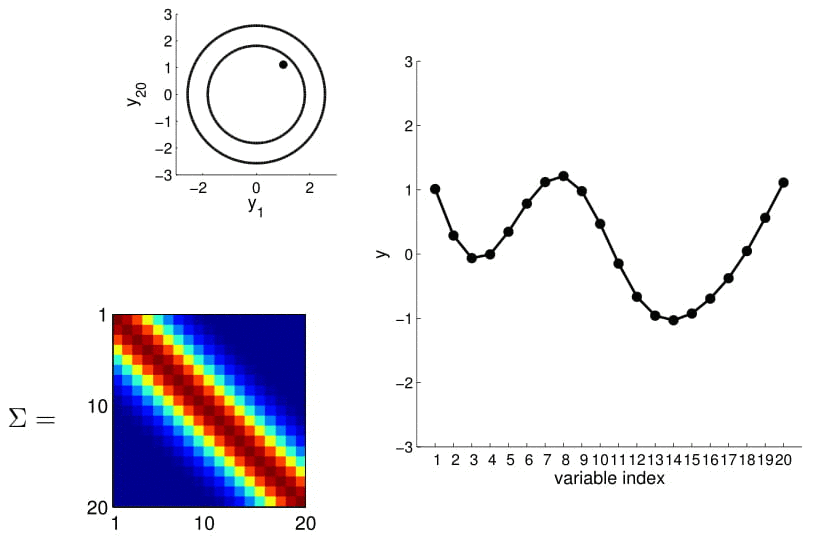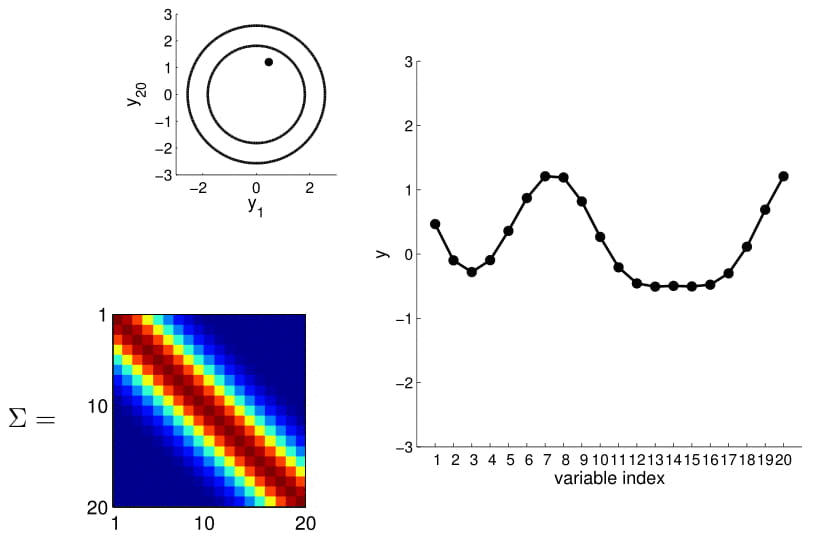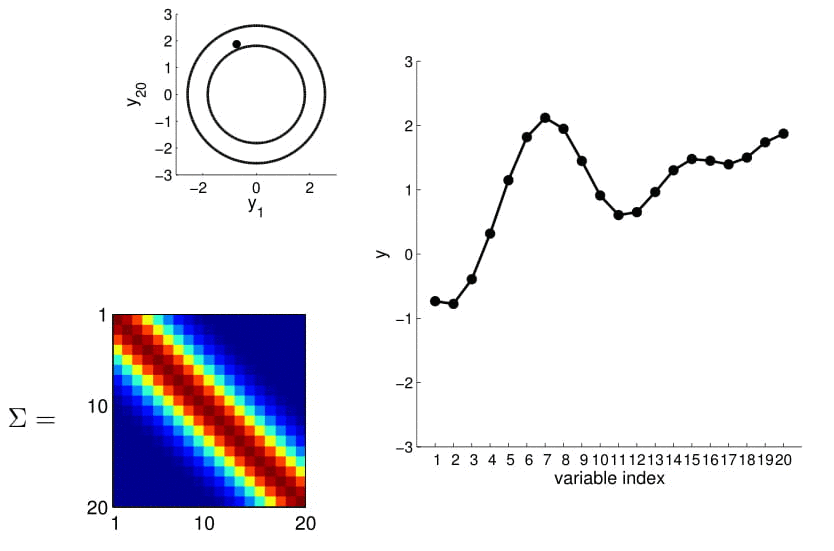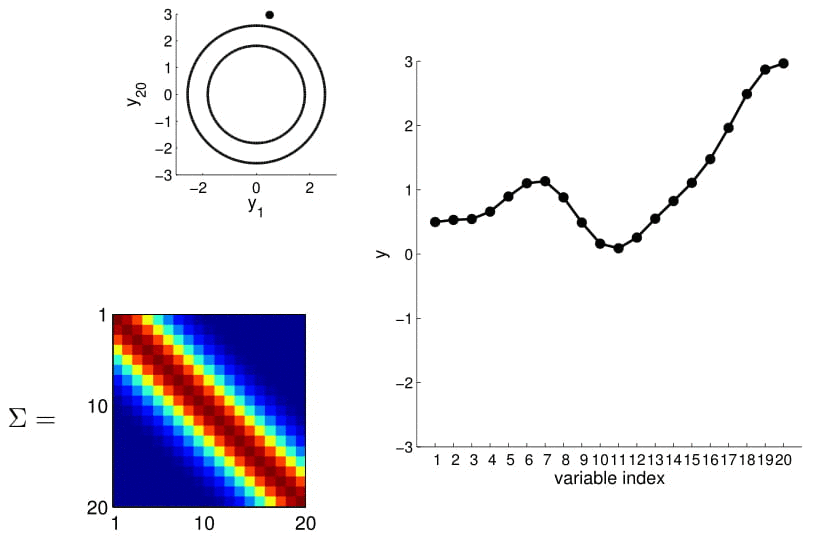
20D Gaussian
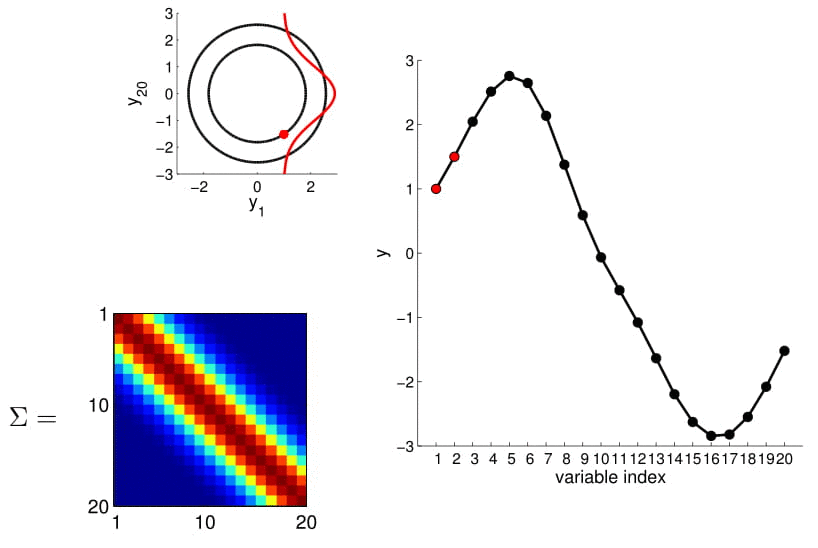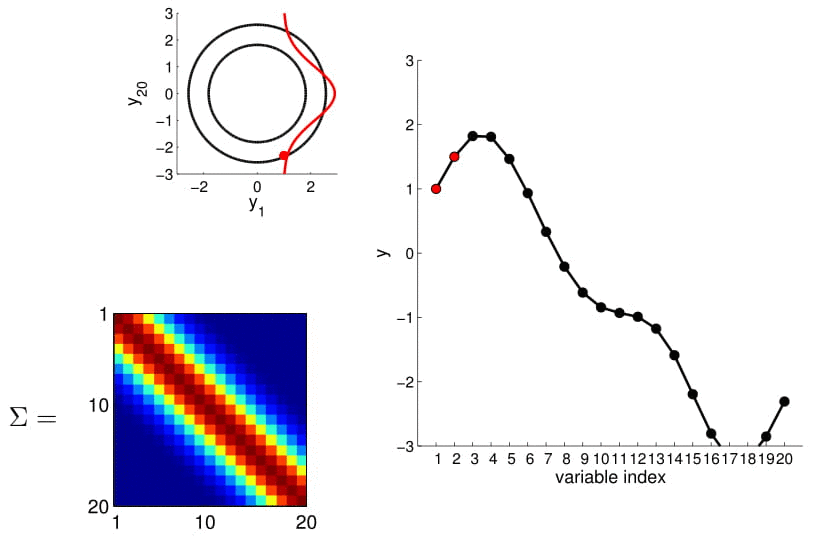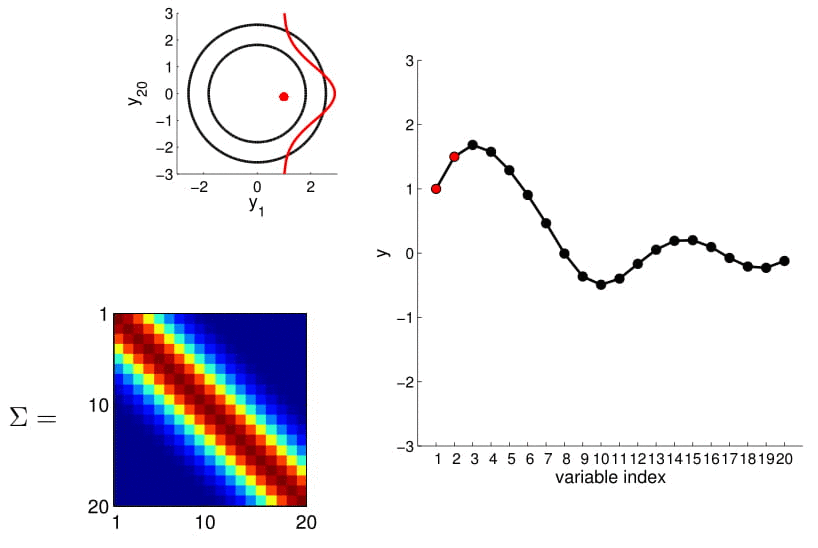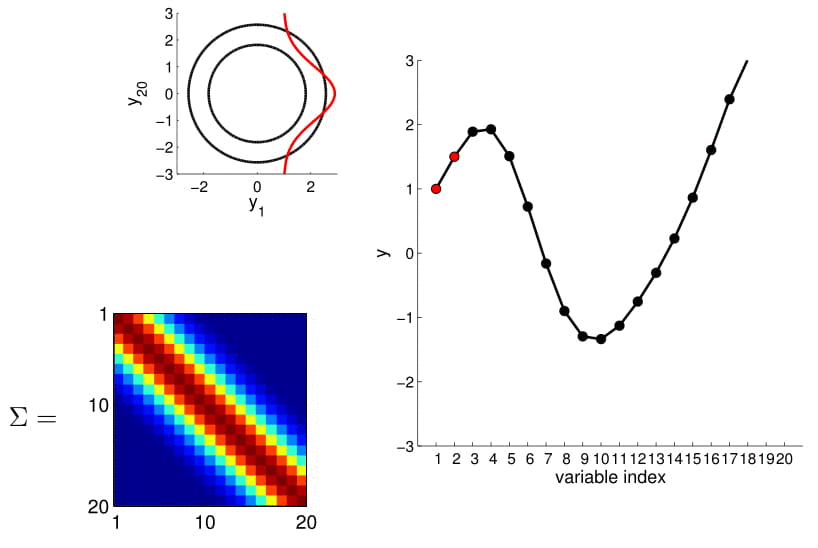
20D Gaussian

Gaussian Process (infinite D)

Hiper-parámetros

Hiper-parámetros

Kernel

Kernel

Kernel

Nuevos datos
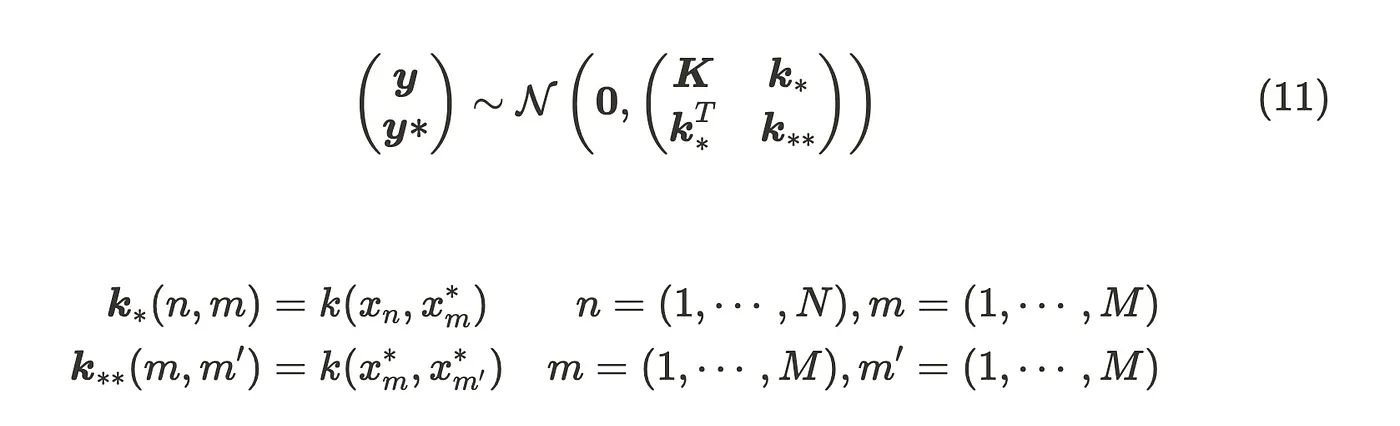
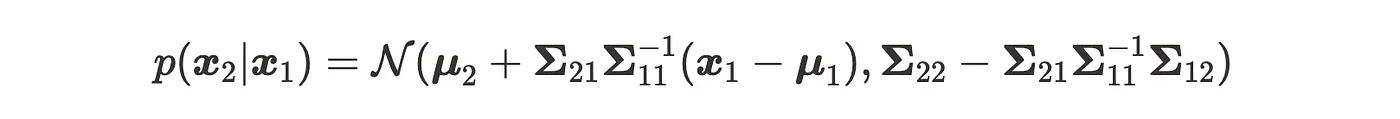
Predicción



Predicción

Predicción


